Question: Suppose that n red dots and n blue dots are drawn in the plane (for some integer n) with no 3 dots in a line.

Suppose that n red dots and n blue dots are drawn in the plane (for some integer n) with no 3 dots in a line. Prove that there *is* a way to connect each red dot to a different blue dot, which minimizes the total length of the line segments? Maybe this seems obvious, but let me remind you that not every set has a minimum element. If I said "okay, now let x be the smallest real number greater than 2", well, that x doesn't exist.

!!!

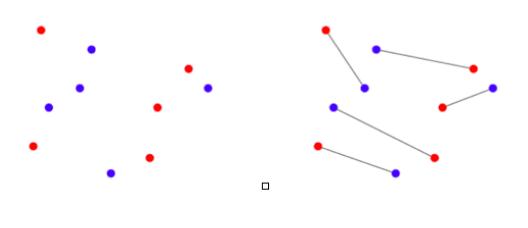
Step by Step Solution

★★★★★

3.45 Rating (155 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

To prove that there is a way to match each red dot with a blue dot such that the sum of the lengths of the line segments is minimized we can make use ... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

Prove that if every even natural number greater than 2 is the sum of two primes, then every odd natural number greater than 5 is the sum of three primes.

There is another way to solve Learning-By-Doing Exercise 12.5. Recall that marginal revenue can be written as MR = P + (P/Q)Q. By factoring out P, we can write Since third-degree price discrimination...

Is it possible for a connected graph drawn in the plane to have an even number of : edges faces, and an odd number of vertices? If yes what would graph look like.

-39-apps-viewer.googleusercontent.com/viewer/secure/pdf/SvtqvoOcne603060ifuf100ak 1t6u211/3817d9c9c1rbro ljrclmm42818teha/1578504000000/drive. CASE 1-1 Starbucks-Going Global Fast The Starbucks...

INSTRUCTIONS six paragraph must include a intro in conclusion talk about each story by itself include what in the story like talk about what all include in that story each story name is bold 1.)...

INSTRUCTIONS six paragraph must include a intro in conclusion each paragraph must be five to seven sentence talk about each story by itself include what in the story like talk about what all include...

Helen Caldicott raises a family and then begins a career as a caterer. As her business grows, she hires several employees and rents space near downtown that has a retail space, parking, and a garage...

CASE EXAMPLE Google: who drives the strategy? Phyl Johnson, Strategy Explorers From an idea to a verb in less than 15 years: 'to Google - to search the Internet' If you are in need of the answer to a...

I need full code for this project. All the resources are found here. The code for lab 3 is: -) https://ucsb csB.github.io/w19 matni/lab/project01/ Goal and Background The goal of this project is to...

On the ratios sheet only nowhere else. I need help finding Earnings per Share of Common Stock, Net income, and cost of goods sold. I did everything else. The pages are listed by the tab for quick...

Stock BFC has an actual return of 14%. Its covariance with the market return is 0.15 and the market variance is 0.10. The market return is 12% and the Rf is 5%. Explain whether investors should buy...

In late 2018, Mike was approached by a representative of a company called Cycle Tech Inc. (CTI) and asked if he would be interested in incorporating its proprietary technology, CycleScape, into PHL's...

NAPSTER'S REVOLUTION Eighteen - year old Shawn "NAPSTER" Fanning, then a freshman at Northeastern University, dropped out of school and founded Napster Inc. (website was at w.w.w.napster.com) in San...

The following statements were printed in journal articles in the field of psychology. Explain to a person who is unfamiliar with the concept of confidence intervals what each statement means. "The...

ntent/7227252/fullscreen/54164648/View ignment A major automotive manufacturer has announced that it will close a manufacturing plant in Ohio. The manufacturer has seen declines in automobile sales...

Imagine it is currently the first day of 2019. The corporate tax rate is 40% and the WACC is estimated to be 13% pa. Suppose also that there is no surplus cash in any year and that Terminal Value...

L ived by user . Saved to this PC Review View We es Icons 3D Models - SmartArt Mailings Chart Screenshot Help Search Get Add-ins W My Add-ins - Wikipedia Link - Bookmark Cross-reference Online Video...

Data 9.2 on page 540 introduces the dataset Cereal, which includes information on the number of grams of fiber in a serving for 30 different breakfast cereals. The cereals come from three different...

The utility that Julie receives by consuming food F and clothing C is given by U(F, C) = FC. For this utility function, the marginal utilities are MUF = C and MUC = F. a) On a graph with F on the...

Consider the congestion pricing problem illustrated in Figure 17.5. a) What is the size of the deadweight loss from the negative externalities if there is no toll imposed during the peak period? b)...

Suppose that you flip a coin. If it comes up heads, you win $10; if it comes up tails, you lose $10. a) Compute the expected value and variance of this lottery. b) Now consider a modification of this...

25. In Exercise 7, Chapter 8, determine an estimate of p from the posterior dis tribution if the loss function is L (a, p) = k(a p)2. How does this differ from the estimate obtained from the prior...

24. If the loss function in a point estimation problem is of the form L (a, 6) 0 1 if | a 9 |

12. Suppose that you are contemplating drilling an oil well, with the following payoff table (in terms of thousands of dollars):