Question
0 1,3,2 1 5,4 2 3 3 2 4 5 5 4,6,7 6 7 Before loop: distTo[0]=0 nodes-{0,1,2,3,4,5,6,7} Loop 1: v= distTo[ ]= edgeTo[ ]=
|
0 | 1,3,2
|
| 1 | 5,4 |
| 2 | 3 |
| 3 | 2 |
| 4 | 5 |
| 5 | 4,6,7 |
| 6 |
|
| 7 |
|
Before loop:
distTo[0]=0
nodes-{0,1,2,3,4,5,6,7}
Loop 1:
v=
distTo[ ]=
edgeTo[ ]=
distTo[ ]=
edgeTo[ ]=
distTo[ ]=
edgeTo[ ]=
nodes={ }
(a) Run Dijkstra's algorithm on this graph to compute the shortest paths between 0 and every other node. For reference, the algorithm is shown on the next page. Use the adjacency list above for the order of the nodes explored and follow the trace format shown before.


(b) Annotated the edges to show the values in edgeTo, and nodes to show the values in distTo.
Part(c) what are the nodes on path from node 0 to node 6?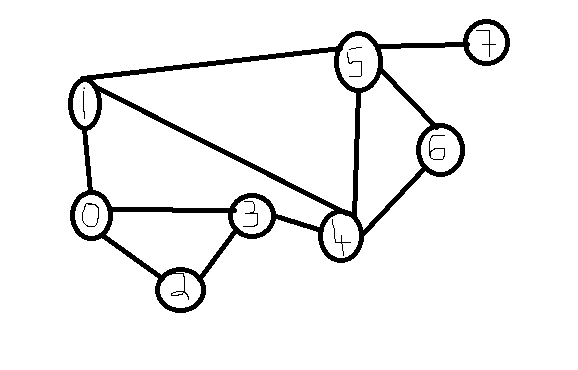
Step by Step Solution
There are 3 Steps involved in it
Step: 1

Get Instant Access to Expert-Tailored Solutions
See step-by-step solutions with expert insights and AI powered tools for academic success
Step: 2

Step: 3

Ace Your Homework with AI
Get the answers you need in no time with our AI-driven, step-by-step assistance
Get Started


