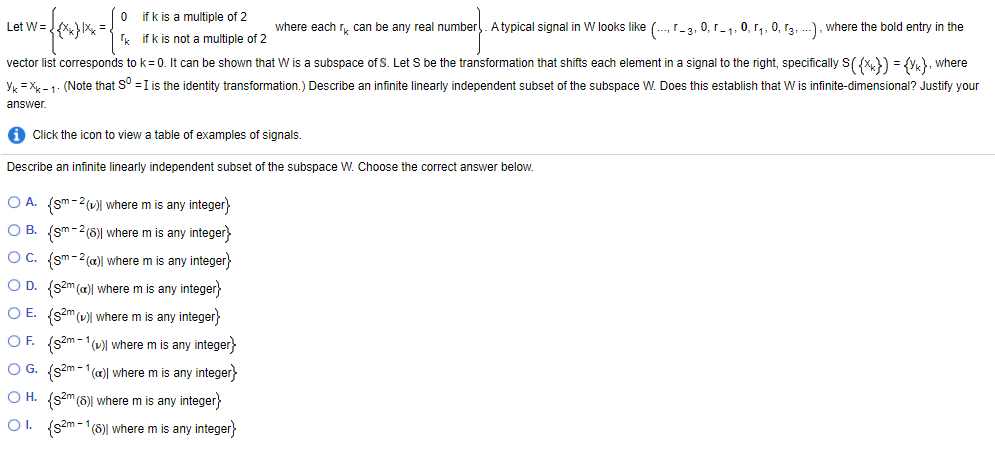
0 if k is a multiple of 2 Let W = {{X}x where each can be any real number. A typical signal in W looks like (-1-3,0,1-1, 0,17,0,13; ...), where the bold entry in the Ik if k is not a multiple of 2 vector list corresponds to k = 0. It can be shown that W is a subspace of S. Let S be the transformation that shifts each element in a signal to the right, specifically S({*}} = {Y"}, where Yk = Xx -7- (Note that S = I is the identity transformation.) Describe an infinite linearly independent subset of the subspace W. Does this establish that W is infinite-dimensional? Justify your answer. Click the icon to view a table of examples of signals Describe an infinite linearly independent subset of the subspace W. Choose the correct answer below. O A. (sm-2(0)| where m is any integer OB. {SM-2(8)| where m is any integer) OC. {sm-2(Q)| where m is any integer) OD. (52m(Q)] where m is any integer} OE. {s2m(w)| where m is any integer) OF {s2m-1()| where m is any integer; OG. {s2m-1(c)] where m is any integer; OH. {s2m (8)| where m is any integer} 01. {s2m-1 (6) where m is any integer; 0 if k is a multiple of 2 Let W = {{X}x where each can be any real number. A typical signal in W looks like (-1-3,0,1-1, 0,17,0,13; ...), where the bold entry in the Ik if k is not a multiple of 2 vector list corresponds to k = 0. It can be shown that W is a subspace of S. Let S be the transformation that shifts each element in a signal to the right, specifically S({*}} = {Y"}, where Yk = Xx -7- (Note that S = I is the identity transformation.) Describe an infinite linearly independent subset of the subspace W. Does this establish that W is infinite-dimensional? Justify your answer. Click the icon to view a table of examples of signals Describe an infinite linearly independent subset of the subspace W. Choose the correct answer below. O A. (sm-2(0)| where m is any integer OB. {SM-2(8)| where m is any integer) OC. {sm-2(Q)| where m is any integer) OD. (52m(Q)] where m is any integer} OE. {s2m(w)| where m is any integer) OF {s2m-1()| where m is any integer; OG. {s2m-1(c)] where m is any integer; OH. {s2m (8)| where m is any integer} 01. {s2m-1 (6) where m is any integer