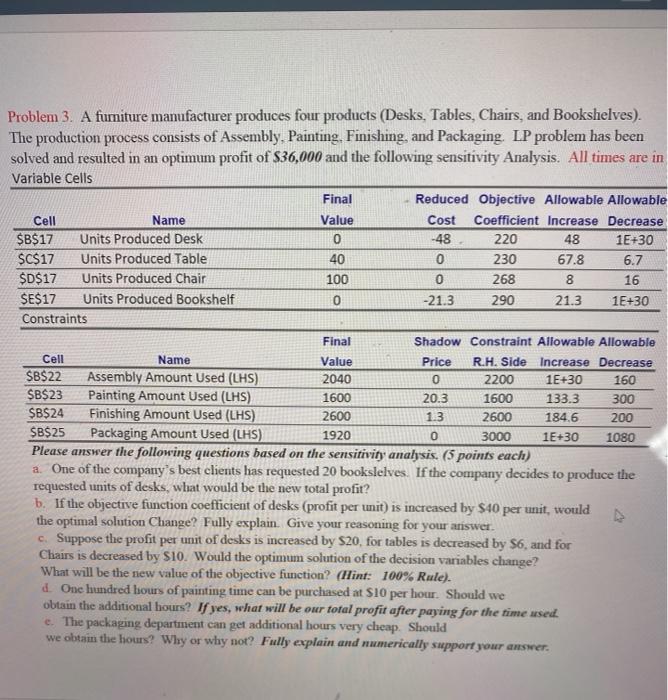
0 Problem 3. A furniture manufacturer produces four products (Desks, Tables, Chairs, and Bookshelves). The production process consists of Assembly, Painting. Finishing, and Packaging. LP problem has been solved and resulted in an optimum profit of $36,000 and the following sensitivity Analysis. All times are in Variable Cells Final Reduced Objective Allowable Allowable Cell Name Value Cost Coefficient Increase Decrease $B$17 Units Produced Desk 0 -48 220 48 1E+30 $C$17 Units Produced Table 40 0 230 67.8 6.7 $D$17 Units Produced Chair 100 268 8 16 SE$17 Units Produced Bookshelf 0 -21.3 290 21.3 1E+30 Constraints Final Shadow Constraint Allowable Allowable Cell Name Value Price R.H. Side Increase Decrease $B$22 Assembly Amount Used (LHS) 2040 2200 1E+30 160 $B$23 Painting Amount Used (LHS) 1600 20.3 1600 133.3 300 $B$24 Finishing Amount Used (LHS) 2600 13 2600 184.6 200 $B$25 Packaging Amount Used (LHS) 1920 0 3000 1E+30 1080 Please answer the following questions based on the sensitivity analysis. (5 points each) a. One of the company's best clients has requested 20 bookslelves. If the company decides to produce the requested units of desks, what would be the new total profit? b. If the objective function coefficient of desks (profit per unit) is increased by S40 per unit, would the optimal solution Change? Fully explain. Give your reasoning for your answer c. Suppose the profit per unit of desks is increased by S20, for tables is decreased by S6, and for Chairs is decreased by S10. Would the optimum solution of the decision variables change? What will be the new value of the objective function? (Hint: 100% Rule). d. One hundred hours of painting time can be purchased at $10 per hour. Should we obtain the additional hours? If yes, what will be our total profit after paying for the time used. e. The packaging department can get additional hours very cheap. Should we obtain the hours? Why or why not? Fully explain and numerically support your answer. 0 0 Problem 3. A furniture manufacturer produces four products (Desks, Tables, Chairs, and Bookshelves). The production process consists of Assembly, Painting. Finishing, and Packaging. LP problem has been solved and resulted in an optimum profit of $36,000 and the following sensitivity Analysis. All times are in Variable Cells Final Reduced Objective Allowable Allowable Cell Name Value Cost Coefficient Increase Decrease $B$17 Units Produced Desk 0 -48 220 48 1E+30 $C$17 Units Produced Table 40 0 230 67.8 6.7 $D$17 Units Produced Chair 100 268 8 16 SE$17 Units Produced Bookshelf 0 -21.3 290 21.3 1E+30 Constraints Final Shadow Constraint Allowable Allowable Cell Name Value Price R.H. Side Increase Decrease $B$22 Assembly Amount Used (LHS) 2040 2200 1E+30 160 $B$23 Painting Amount Used (LHS) 1600 20.3 1600 133.3 300 $B$24 Finishing Amount Used (LHS) 2600 13 2600 184.6 200 $B$25 Packaging Amount Used (LHS) 1920 0 3000 1E+30 1080 Please answer the following questions based on the sensitivity analysis. (5 points each) a. One of the company's best clients has requested 20 bookslelves. If the company decides to produce the requested units of desks, what would be the new total profit? b. If the objective function coefficient of desks (profit per unit) is increased by S40 per unit, would the optimal solution Change? Fully explain. Give your reasoning for your answer c. Suppose the profit per unit of desks is increased by S20, for tables is decreased by S6, and for Chairs is decreased by S10. Would the optimum solution of the decision variables change? What will be the new value of the objective function? (Hint: 100% Rule). d. One hundred hours of painting time can be purchased at $10 per hour. Should we obtain the additional hours? If yes, what will be our total profit after paying for the time used. e. The packaging department can get additional hours very cheap. Should we obtain the hours? Why or why not? Fully explain and numerically support your answer. 0