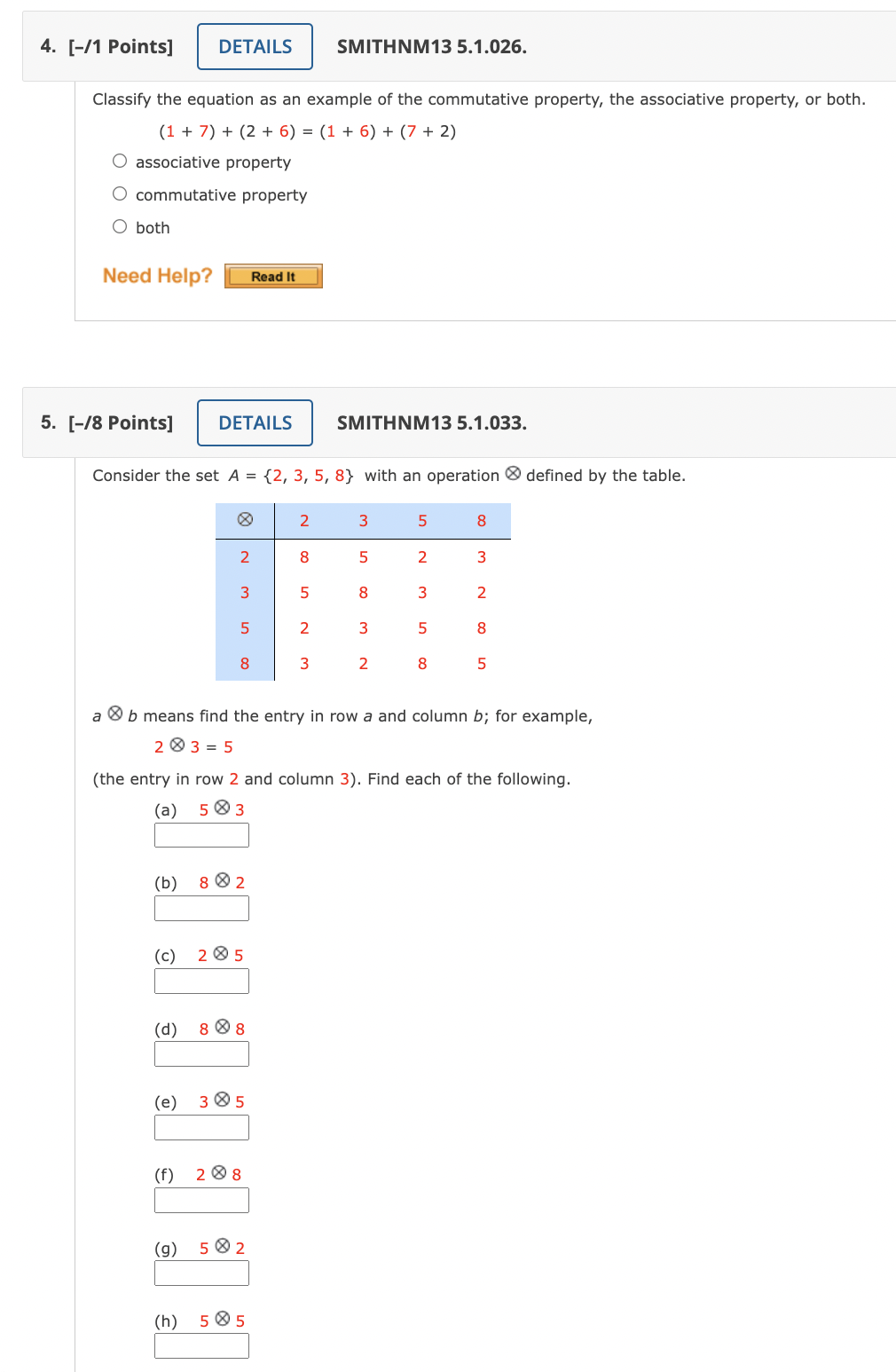
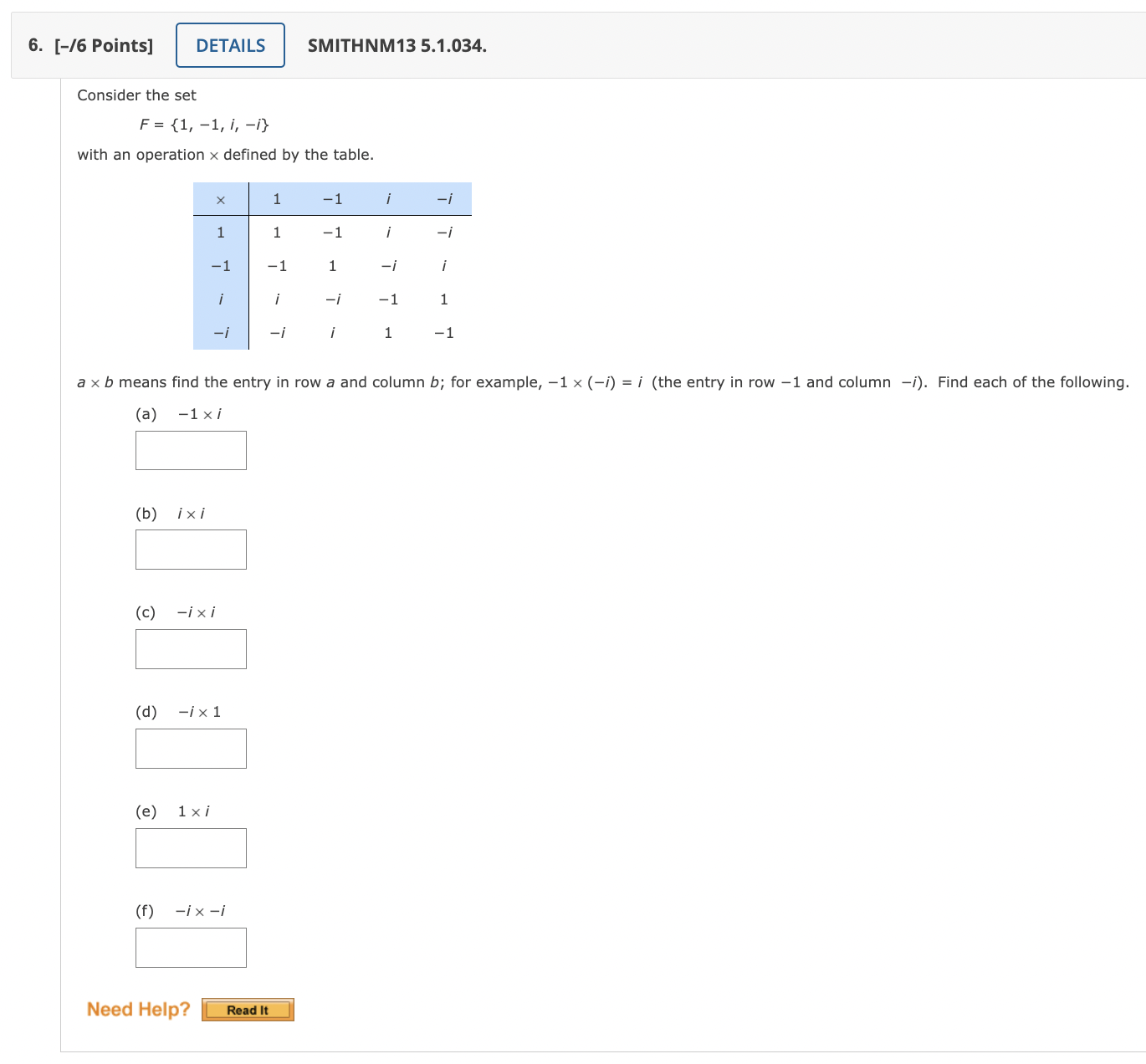
1. [-11 Points] DETAILS SMITHNM13 5.1.018. Classify the equation as an example of the commutative property, the associative property, or both. 6+{2+3)=(6+2)+3 O associative property 0 commutative property 0 both Need Help? _ 2. [-11 Points] DETAILS SMITHNM13 5.1.020. I MY NOTE Classify the equation as an example of the commutative property, the associative property, or both. 9+{5+4)=9+(4+5) O associative property O commutative property 0 both Need Help? _' _' 3. [-11 Points] DETAILS SMITHNM13 5.1.024. Classify the equation as an example of the commutative property, the associative property, or both. (3+5)+(2+4)=(3+5)+{4+2) O associative property 0 commutative property 0 both Need Help? _ 4. [-/1 Points] DETAILS SMITHNM13 5.1.026. Classify the equation as an example of the commutative property, the associative property, or both. (1 + 7) + (2 + 6) = (1+ 6)+ (7+ 2) O associative property O commutative property O both Need Help? Read It 5. [-/8 Points] DETAILS SMITHNM13 5.1.033. Consider the set A = {2, 3, 5, 8} with an operation & defined by the table. X 2 3 5 8 U w N N 3 5 8 3 2 5 2 3 5 8 8 3 2 8 UT a & b means find the entry in row a and column b; for example, 20 3 = 5 (the entry in row 2 and column 3). Find each of the following. (a) 503 ) 802 (c) 205 (d) 8 8 8 e) 385 (f) 208 (9) 502 (h) 5056. [-/6 Points] DETAILS SMITHNM13 5.1.034. Consider the set F = {1, -1, i, -i} with an operation x defined by the table. X 1 -1 i -1 -1 1 -i 1 -1 a x b means find the entry in row a and column b; for example, -1 x (-/) = / (the entry in row -1 and column -/). Find each of the following. (a) -1 x/ ixi (c) -ixi (d) -ix 1 (e) 1xi (f ) -ix -i Need Help? Read It7. [-/4 Points] DETAILS SMITHNM13 5.1.043. Consider the operation . defined by the following table. 0 4 O O 4 A A O O A O a . b means find the entry in row a and column b. (a) Find . A Oo O A (b) Find A . O. Oo O A (c) Does o . = . o? O Yes O No (d) Is the set commutative for .? O Yes O No Need Help? Read It 8. [-/1 Points] DETAILS SMITHNM13 5.1.045A. Let + mean "select the smaller number" and - mean "select the second of the two." Is - distributive over $ in the set of natural numbers, N? O Yes O No Need Help? Read It9. [-/2 Points] DETAILS SMITHNM13 5.1.048. Consider the set 7 = {0, 1}. (a) Is T commutative for the operation of multiplication? Yes O No (b) Is T associative for the operation of multiplication? O Yes O No Need Help? Read It 10. [-/2 Points] DETAILS SMITHNM13 5.1.052. (a) Is the set of multiples of three closed for addition? O Yes O No (b) Is the set of multiples of three closed for multiplication? O Yes O No Need Help? Read It 11. [-/1 Points] DETAILS SMITHNM13 5.1.053. Let S = {1, 2, 3, . . . , 9, 10}. Define an operation o as a ob = 1 . a + 0 . b. Is S closed for the operation of o? O Yes O No Need Help? Read It12. [-/1 Points] DETAILS SMITHNM13 5.1.054. MY NOTES ASK Y Let S = {1, 2, 3, . . ., 99, 100}. Define an operation e as a ob = 2a + b. Check the commutative and associative properties. It is commutative, but not associative. O It is neither associative nor commutative. It is associative, but not commutative. O It is both associative and commutative. Need Help? Read It 13. [-/15 Points] DETAILS SMITHNM13 5.1.056. MY NOTES ASK Y Consider a soldier facing in a given direction (say north). Let us denote "left face" by l, "right face" by r, about face" by a, and "stand fast" by f. (The element f means "don't move from your present position." It does not mean "return to your original position.") Then we define H = {l, r, a, f} and an operation meaning "followed by." Thus, { *{ = a means "left face" followed by "left face" and is the same as the single command "about face." Complete the following table. a a a Need Help? Read It