1 2.
2.
3.
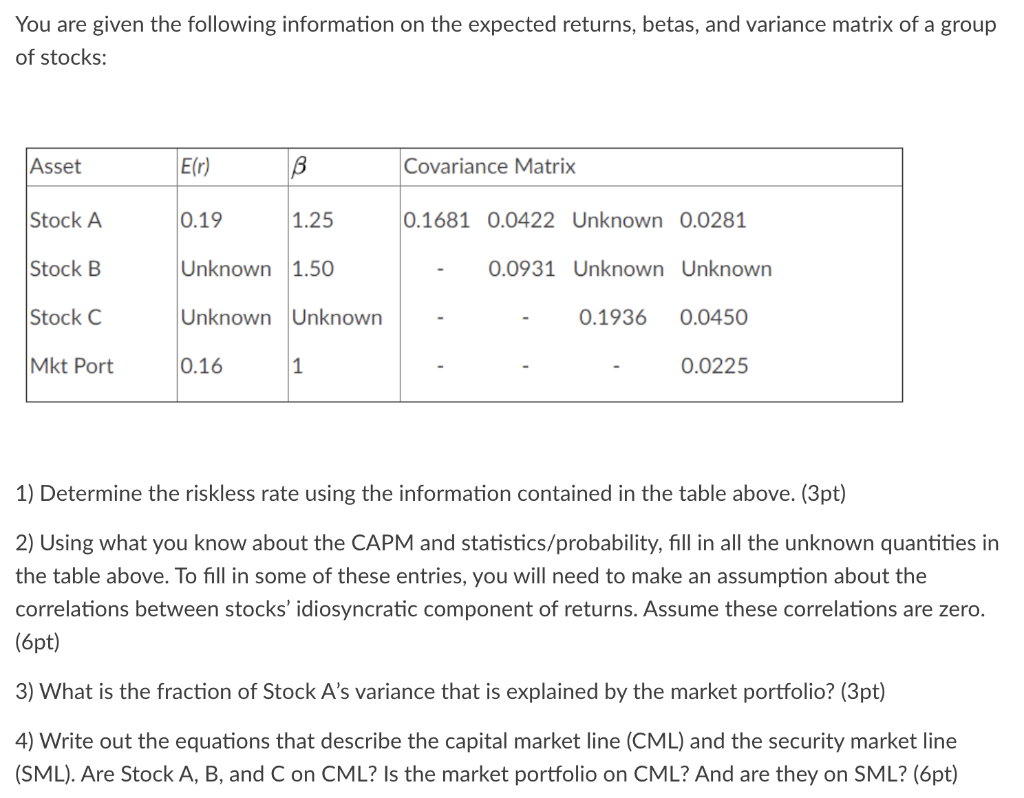
Suppose we have three stocks: A, B and C. Their expected returns are given by r = [0.21 0.11 0.21 The covariance matrix is 1 0 0 V 0 0.5 0 0 0 1 1) Find the Global Minimum Variance (GMV) Portfolio. (4pt) 2) Another portfolio on the MVF is the equal-weighted portfolio: XA = XB = xc = 1/3. Using your answer in part (1) and the two fund separation theorem, find the portfolio on the MVF with an expected return of 15.5%. (4pt) 3) Suppose the risk-free rate is 1%. What is the Mean Variance Efficient (MVE) portfolio? (4pt) 4) Consider a mean-variance investor with a risk aversion coefficient of 3. Now he needs to allocate $ 20 millions to the risk-free asset and these three stocks. What amount would he put into each stock? (4pt) You are given the following information on the expected returns, betas, and variance matrix of a group of stocks: Asset E(r) B Covariance Matrix Stock A 0.19 1.25 0.1681 0.0422 Unknown 0.0281 Stock B Unknown 1.50 0.0931 Unknown Unknown Stock C Unknown Unknown 0.1936 0.0450 Mkt Port 0.16 1 0.0225 1) Determine the riskless rate using the information contained in the table above. (3pt) 2) Using what you know about the CAPM and statistics/probability, fill in all the unknown quantities in the table above. To fill in some of these entries, you will need to make an assumption about the correlations between stocks' idiosyncratic component of returns. Assume these correlations are zero. (6pt) 3) What is the fraction of Stock A's variance that is explained by the market portfolio? (3pt) 4) Write out the equations that describe the capital market line (CML) and the security market line (SML). Are Stock A, B, and C on CML? Is the market portfolio on CML? And are they on SML? (6pt) Suppose the economy is described by a three-factor model. Consider three well-diversified portfolios A, B and C, which do not have any idiosyncratic risk. The risk exposures of portfolio A to factors F1, F2 and F3 are BA1 = 0, $A2 = 1 and A3 = 0. For portfolio B, the corresponding exposures are BB1 = 1, BB2 = 1, BB3 = 1. For portfolio C, the corresponding exposures are ci = 2, Bc2 = 0, Bc3 = 1. Let RP 1, RP2, and RP3 denote the risk premia on the three factor portfolios. 1) Using the information above, write down the "pricing equation" for portfolio A, portfolio B and portfolio C in this three-factor pricing model. That is, what is the risk premium of each portfolio as a function of RP1, RP2 and RP3? (6pt) 2) Construct a portfolio by mixing A, B and (and nothing else) to replicate the systematic risk of the first pricing factor F3. Find the weights of this portfolio. (6pt) 3) Suppose that you have estimated the risk premium on portfolio A is 3%, the risk premium on portfolio B is 6%, and the risk premium on portfolio C is 4%. If there is no arbitrage, what are the risk premia on the three factor portfolios? (6pt) Edit View Insert Format Tools Table Suppose we have three stocks: A, B and C. Their expected returns are given by r = [0.21 0.11 0.21 The covariance matrix is 1 0 0 V 0 0.5 0 0 0 1 1) Find the Global Minimum Variance (GMV) Portfolio. (4pt) 2) Another portfolio on the MVF is the equal-weighted portfolio: XA = XB = xc = 1/3. Using your answer in part (1) and the two fund separation theorem, find the portfolio on the MVF with an expected return of 15.5%. (4pt) 3) Suppose the risk-free rate is 1%. What is the Mean Variance Efficient (MVE) portfolio? (4pt) 4) Consider a mean-variance investor with a risk aversion coefficient of 3. Now he needs to allocate $ 20 millions to the risk-free asset and these three stocks. What amount would he put into each stock? (4pt) You are given the following information on the expected returns, betas, and variance matrix of a group of stocks: Asset E(r) B Covariance Matrix Stock A 0.19 1.25 0.1681 0.0422 Unknown 0.0281 Stock B Unknown 1.50 0.0931 Unknown Unknown Stock C Unknown Unknown 0.1936 0.0450 Mkt Port 0.16 1 0.0225 1) Determine the riskless rate using the information contained in the table above. (3pt) 2) Using what you know about the CAPM and statistics/probability, fill in all the unknown quantities in the table above. To fill in some of these entries, you will need to make an assumption about the correlations between stocks' idiosyncratic component of returns. Assume these correlations are zero. (6pt) 3) What is the fraction of Stock A's variance that is explained by the market portfolio? (3pt) 4) Write out the equations that describe the capital market line (CML) and the security market line (SML). Are Stock A, B, and C on CML? Is the market portfolio on CML? And are they on SML? (6pt) Suppose the economy is described by a three-factor model. Consider three well-diversified portfolios A, B and C, which do not have any idiosyncratic risk. The risk exposures of portfolio A to factors F1, F2 and F3 are BA1 = 0, $A2 = 1 and A3 = 0. For portfolio B, the corresponding exposures are BB1 = 1, BB2 = 1, BB3 = 1. For portfolio C, the corresponding exposures are ci = 2, Bc2 = 0, Bc3 = 1. Let RP 1, RP2, and RP3 denote the risk premia on the three factor portfolios. 1) Using the information above, write down the "pricing equation" for portfolio A, portfolio B and portfolio C in this three-factor pricing model. That is, what is the risk premium of each portfolio as a function of RP1, RP2 and RP3? (6pt) 2) Construct a portfolio by mixing A, B and (and nothing else) to replicate the systematic risk of the first pricing factor F3. Find the weights of this portfolio. (6pt) 3) Suppose that you have estimated the risk premium on portfolio A is 3%, the risk premium on portfolio B is 6%, and the risk premium on portfolio C is 4%. If there is no arbitrage, what are the risk premia on the three factor portfolios? (6pt) Edit View Insert Format Tools Table
 2.
2.







