1.
2.
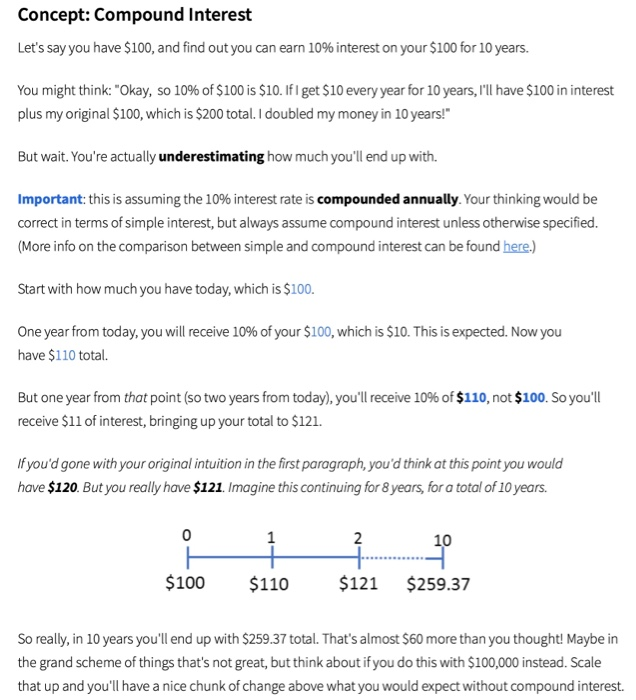
Concept: Compound Interest Let's say you have $100, and find out you can earn 10% interest on your $100 for 10 years. You might think: "Okay, so 10% of $100 is $10. If I get $10 every year for 10 years, I'll have $100 in interest plus my original $100, which is $200 total. I doubled my money in 10 years! But wait. You're actually underestimating how much you'll end up with. Important: this is assuming the 10% interest rate is compounded annually. Your thinking would be correct in terms of simple interest, but always assume compound interest unless otherwise specified. (More info on the comparison between simple and compound interest can be found here.) Start with how much you have today, which is $100. One year from today, you will receive 10% of your $100, which is $10. This is expected. Now you have $110 total. But one year from that point (so two years from today), you'll receive 10% of $110, not $100. So you'll receive $11 of interes, bringing up your total to $121 If you'd gone with your original intuition in the first paragraph, you'd think at this point you would have $120. But you really have $121. Imagine this continuing for 8 years, for a total of 10 years. 0 10 $100 $110 $121 $259.37 So really, in 10 years you'll end up with $259.37 total. That's almost $60 more than you thought! Maybe in the grand scheme of things that's not great, but think about if you do this with $100,000 instead. Scale that up and you'll have a nice chunk of change above what you would expect without compound interest. You start out with $10 and find out you can earn 10% interest on your money for the next 25 years. How much interest will you have earned after 25 years? Round to the nearest cent. Formula: Future Value of an Annuity with Non-Annual Cash Flows Start with the formula for the FV of an Annuity: (1 i)1 FVannuityCF FV Future Value CF amount per period i interest rate n number of periods Let's say that instead of $5,000 each year for 5 years with an interest rate of 7%, you have to figure out the future value of $500 invested each month for 5 years with an interest rate of 7%. So far, you have this information to set up the problem FV=? CF $500 per month n 5 years . i: 796 (annual rate) Important: unless otherwise stated, the given interest rate in each question is an annual rate. This means that if you have compounding periods that aren't in terms of years (in this case, you're compounding in months because you're getting cash on a monthly basis), then you have to adjust both the term n and the term i Let's start with term n, which s currently inyears.This term basically sates how many times your money is being compounded. Right now, n 5 means that your money is being compounded once a year for 5 years. However, the cash flows are occurring monthly.If you invest $500 in January, that will earn 11 months of interest.We can't just pretend cash flows are annual and ignore that interest. But if you want it to reflect monthly compounding you multiply it by 12, because there are 12 months in 1 year. 12 5-60 months, so n 60 which means your money is being compounded once a month for5 years. Now we have this: FV-? . CF $500 per month n 60 months i : 7% (annual rate) . One more adjustment: the interest rate. To get the interest rate to monthly terms, divide the 7% by 12 months. This gives you a new interest rate of 0.0583396 All together, your inputs are now: FV-? CF $500 per month . n 60 months . 1-796 / 12-0.5833% per month Now that everything is in common terms, substitute the values above into the FV of an Annuity shortcut: 0.005833 Watch the decimals after making the adjustment! The solution is $35,796.45. If you're not getting thisnumberor anything close to it, try putting it in your calculator again. Sometimes you can be misplacing parentheses or mistyping some numbers. You land a babysitting job that promises to pay $100 per month. If you expect to have the job for the next 4 years and earn interest of 496, how much will you have in 4 years? Round to the nearest cent












