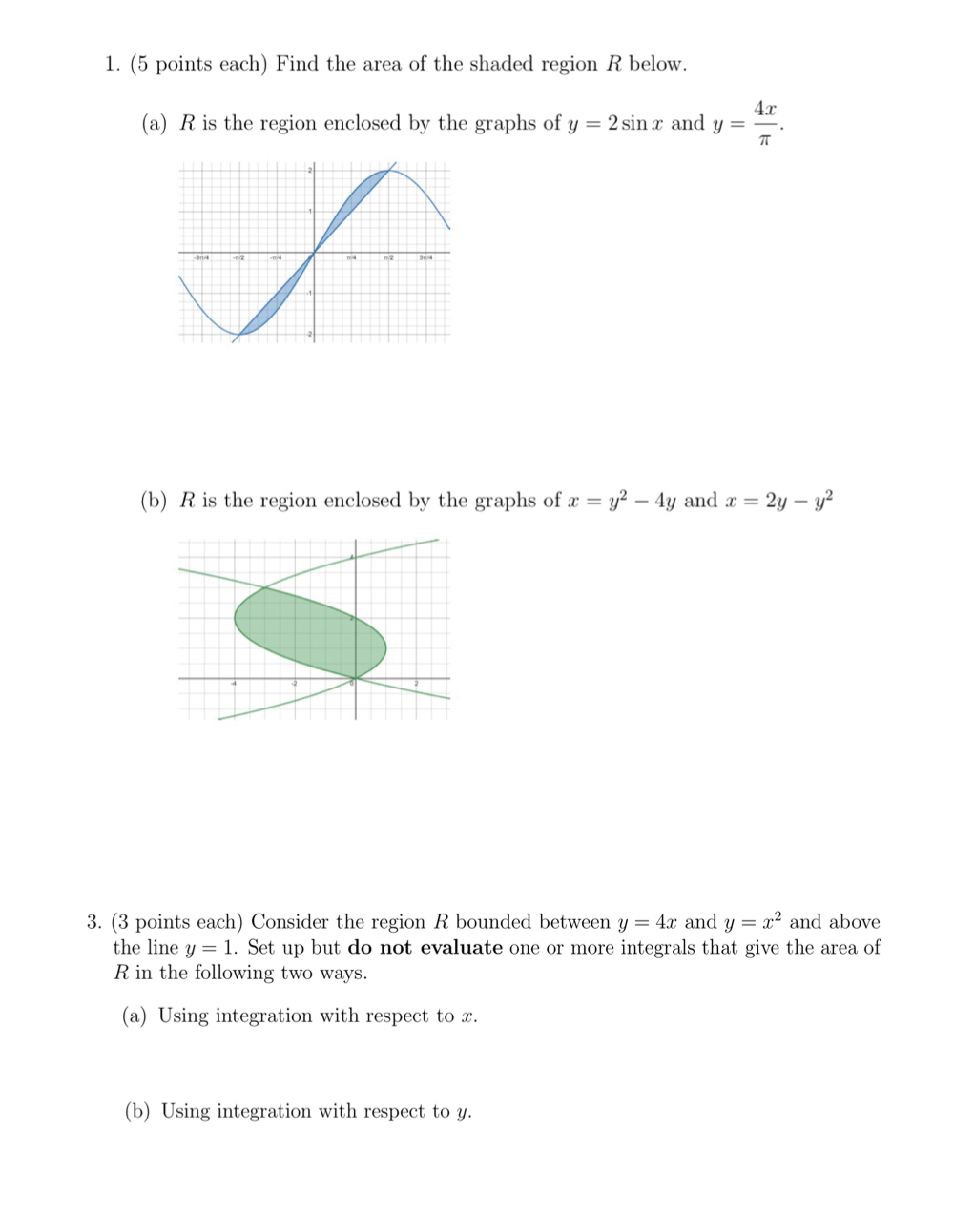
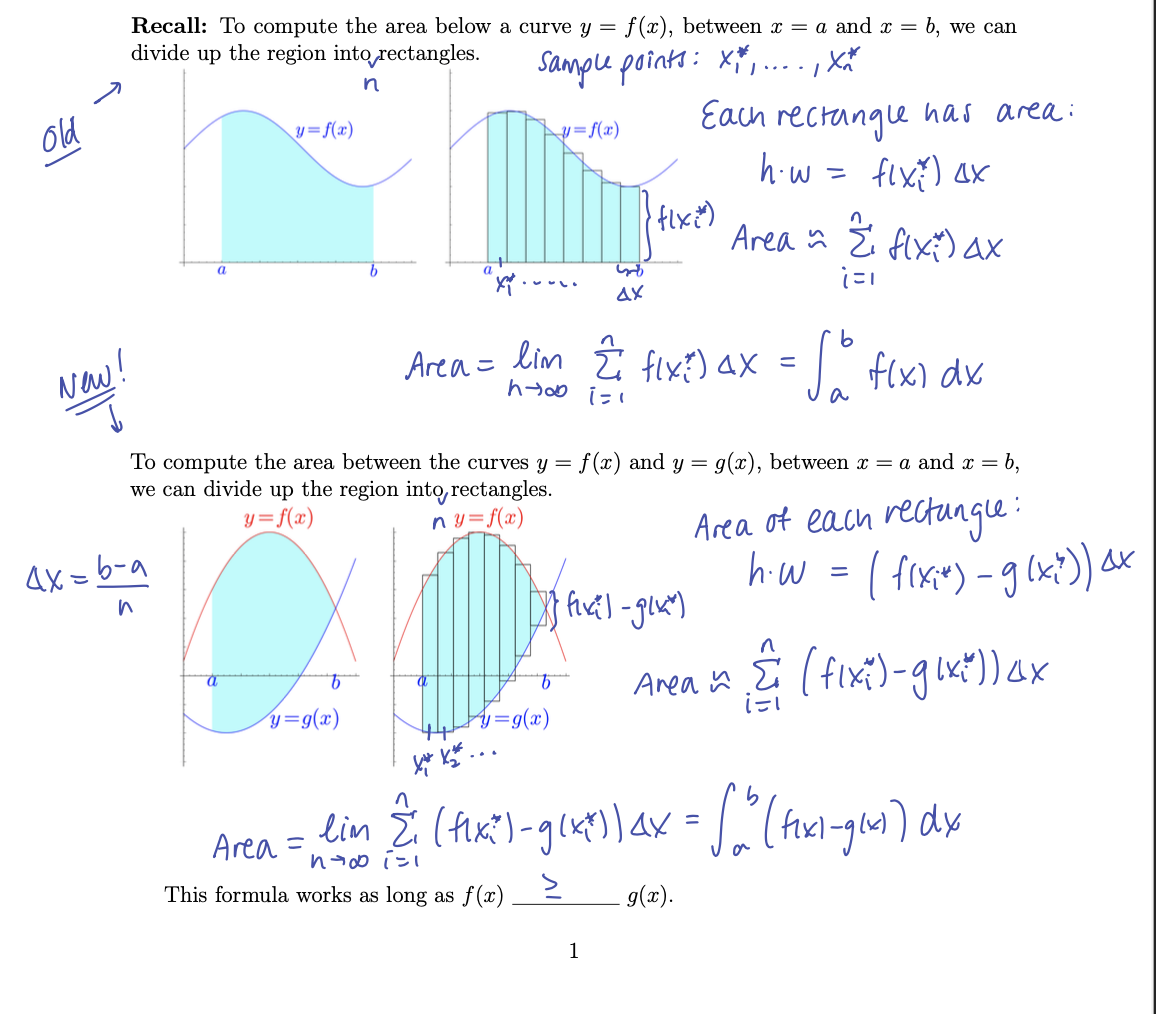
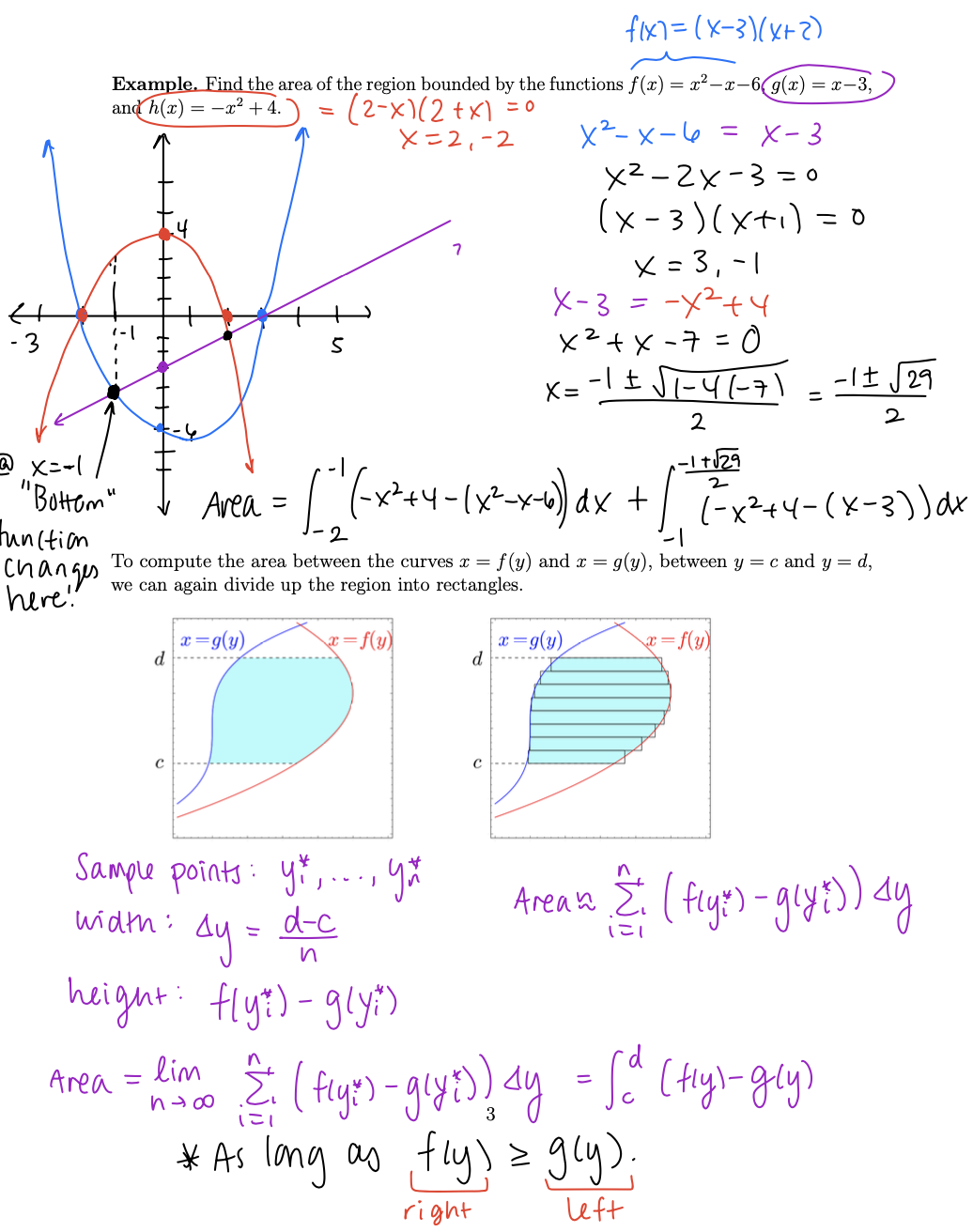
1. (5 points each) Find the area of the shaded region R below. (a) R is the region enclosed by the graphs of y = 2 sin x and y = m2 34 4x (b) R is the region enclosed by the graphs of x = y-4y and x = 2y-y2 3. (3 points each) Consider the region R bounded between y = 4x and y = x and above the line y 1. Set up but do not evaluate one or more integrals that give the area of R in the following two ways. (a) Using integration with respect to x. (b) Using integration with respect to y. Old Recall: To compute the area below a curve y = f(x), between x = a and x = b, we can divide up the region into rectangles. n y=f(x) a b Sample points: x, y= f(x) AX xxx Each rectangle has area: hw = fix?) ax flx) = Area = f(x) Ax i=1 b Area = lim & fix?) ax = o flx) dx 1=1 a0f4 a To compute the area between the curves y = f(x) and y = g(x), between x = a and x = b, we can divide up the region into rectangles. New! ax. = n b-a a y= f(x) ny= f(x) (fivil-glxm Area of each rectangle: hw = (f(xit) - g (xi)) ax Area ~ (fixi) - glx")) ax y= g(x) =g(x) Area = lim & (fix") - g(x^)) ax = " (fixl-g(x)) dx This formula works as long as f(x) 1 g(x). Area = d = 3x red bottom blue Example. Find the area between the curves y = x + x and y = 3x. -3 -2/1 top Set them equal to find endpoints: y=3-x 2 3-x = x+x 0=2x+x-3 t 0 = (2x+3)(x-1) 11312 ( 3-x - (x + x)) dx = 1312 = 3 - 2/35 3 X = 1, -1 (3-2x-x) dx = 3---()-()3-()) 2 X - x -312 9 71 - + + = + = 2 24 Example. Find the area between the curves y = 2x + 1 and y = 5 - 2x. >9=2x+1 |4=5-2x 2x+1=5-2x2 2x+2x-4=0 x+x-2=0 (x+2)(X-1) = x= -2,1 bottan i top Area = (5-2x- (2x+1)) dx = [" (4-2x-2x) dx = 4x - = 4- -1 -(4(-2)-2-3-(-2) -(-2)) 2 2 = 3 = - 2/3 8-16 3 +81 +4-15-13-15-6-9 H m f1x7=(x-3)(x+2) Example. Find the area of the region bounded by the functions f(x) = x-x-6(g(x) = x-3, and h(x) = x+4. = (2-x)(2+x) x=2,-2 = 0 7 x-x-6=x-3 x-2x-3= 0 (x-3)(x+1)=0 x = 3-1 5 X-3 = -x+4 x= x+x-7=0 -11-41-71 -129 = 2 2 X=-1 "Bottom" unction Changes here! Area = [ " (-x + 4 = (x-x-6), 2 -1+29 2 dx + (-x+4-(x-3))dx To compute the area between the curves x = f(y) and x = g(y), between y = c and y = d, we can again divide up the region into rectangles. x=g(y) d C x=f(y) x=9(y) x= f(y) d C Sample points: y,..., yu width: Ay = d-c n height: fly?)-gly") Area lim = n o n Arean & (fly:) - gly :)) gly); right left