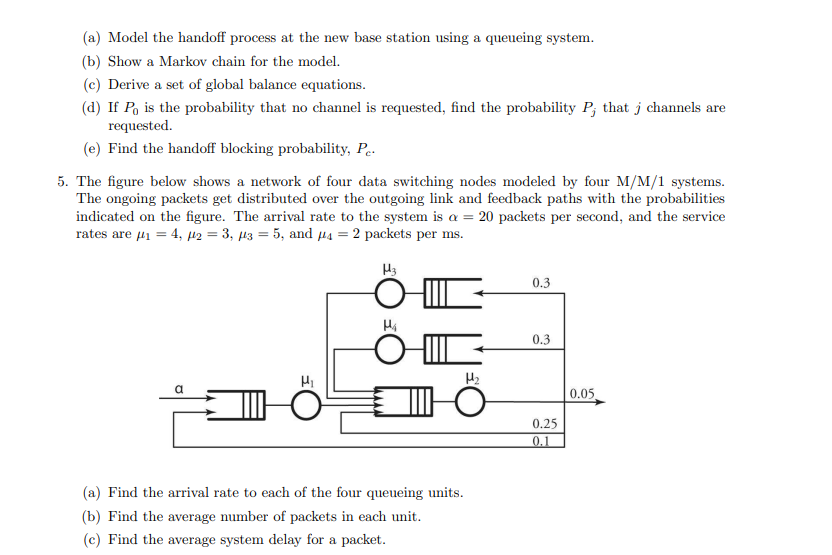
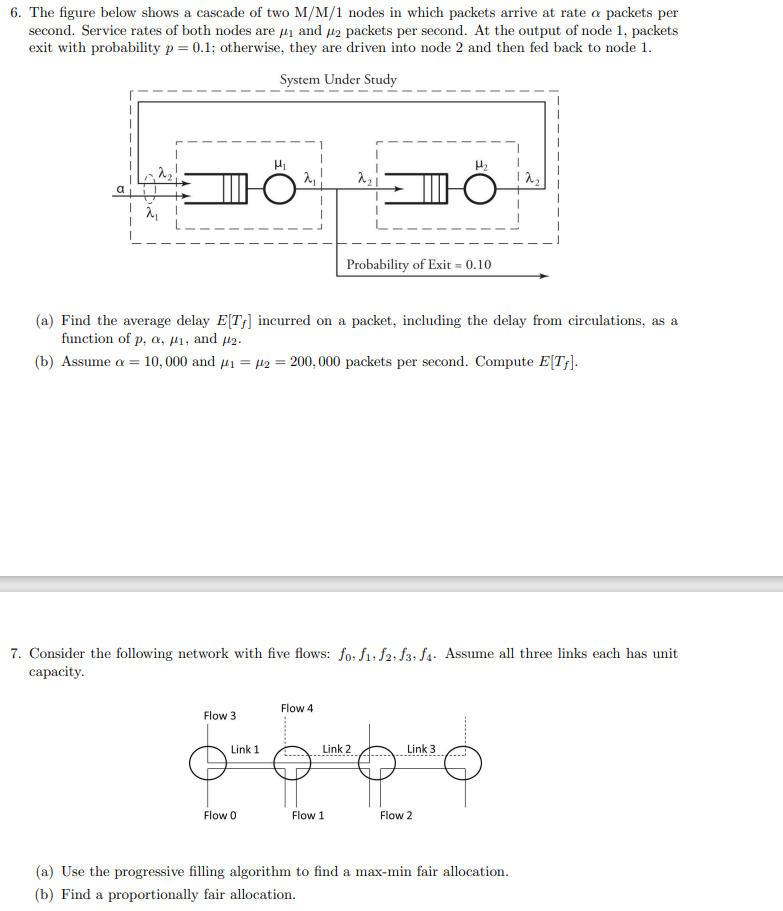
1. A communication link whose transmission rate is 50Kbits per second is used to support 10 flows each generating Poisson traffic at a rate of 150 packets per minutes. Packet lengths (of all flows) are exponentially distributed with mean 1000 bits. (a) Assume that all 10 flows send their traffic through the same link using statistical multiplexing. Note that aggregating n independent Poisson processes into one single process results in a Poisson process whose rate is the sum of the rates of the n aggregated processes. Using a continuous-time M/M/1 queuing system, find: i. The average number of packets in the system. ii. The average delay a packet spends in the system. iii. The average delay a packet spends in the queue. iv. The average number of packets in the queue. (b) Assume that 10 equal-capacity time-division multiplexed channels are created, each to support one flow all independent from one another. Answer all questions of part (a) above for this system. (c) Compare results obtained from (a) and (b) and comment on whether and when statistical multi- plexing is more efficient than time-division (or frequency-division) multiplexing. 2. Consider a network node represented by an M/M/1 model. (a) Find the probability that the number of packets in the node is less than a given number k, P[K(t) (a) Model the handoff process at the new base station using a queueing system. (b) Show a Markov chain for the model. (c) Derive a set of global balance equations. (d) If Po is the probability that no channel is requested, find the probability P; that j channels are requested. (e) Find the handoff blocking probability, P. 5. The figure below shows a network of four data switching nodes modeled by four M/M/1 systems. The ongoing packets get distributed over the outgoing link and feedback paths with the probabilities indicated on the figure. The arrival rate to the system is a = 20 packets per second, and the service rates are = 4, 2 = 3, 3 = 5, and 4 = 2 packets per ms. H3 H H4 (a) Find the arrival rate to each of the four queueing units. (b) Find the average number of packets in each unit. (c) Find the average system delay for a packet. 0.3 0.3 0.25 0.1 0.05 6. The figure below shows a cascade of two M/M/1 nodes in which packets arrive at rate a packets per second. Service rates of both nodes are and 2 packets per second. At the output of node 1, packets exit with probability p = 0.1; otherwise, they are driven into node 2 and then fed back to node 1. System Under Study Flow 3 H 21 Link 1 Flow 0 (a) Find the average delay E[T] incurred on a packet, including the delay from circulations, as a function of p, a, #1, and 2. (b) Assume a = 10,000 and = 2 = 200,000 packets per second. Compute E[T]. 2 7. Consider the following network with five flows: fo, f1, f2, f3, f4. Assume all three links each has unit capacity. Flow 4 Probability of Exit = 0.10 Link 2 0-0-0-0 Flow 1 H O Link 3 Flow 2 2 (a) Use the progressive filling algorithm to find a max-min fair allocation. (b) Find a proportionally fair allocation.