1. (a) Find the shortest weighted path from C to all other vertices in graph 2 using Dijkstra's algorithm. List both the nodes on each path and the cost of each path. (b) Specify what the dist field for each node is immediately after node D has been selected off of the priority queue (but not processed). 2. Show how to modify Dijkstra's algorithm to count the number of minimum costs paths from the source vertex s to all other vertices. 3. One idea to find minimum cost paths in graphs with negative weights (but still no negative cycles) is the following: Add a constant value c to all edge weights so that there are no negative weights and then use Dijkstra's algorithm to nd the minimum cost paths. Either prove that this approach works or find a small counter example that shows that it won't work. 4. Consider the following statement: If a directed graph G = (V;E) is acyclic and no edge between u and v is in E, then at least one of (u; v) or (v; u) can be added to E without creating a cycle. Give a (short) proof that this statement is correct or find a counterexample.

Dijkstra's algorithm

void dijkstra (vertix s)

cleandata();

s.dist =0 ;

pq.insert(s);

while (!pq.isEmpty()) {

v= pq.deletMin();

if (v.visited)

continue;

v.visited = true;

for (all (v,w) 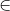E) {

if(v.dist + e.cost

w.dist = v.dist + e.cost;

w.prev = v;

pq.enque(w);

}

}

}

}

Graph 2 Graph 2