Question: 1 A function f(x) is called shift-scale-invariant if, for every x0, there exists a value such that y = f(x) implies y = f(x'),

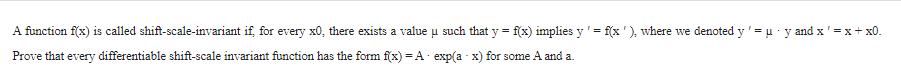
1 A function f(x) is called shift-scale-invariant if, for every x0, there exists a value such that y = f(x) implies y = f(x'), where we denoted y'=uy and x'=x+x0. Prove that every differentiable shift-scale invariant function has the form f(x) = A exp(a - x) for some A and a.

Step by Step Solution

★★★★★

3.46 Rating (162 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

Let fx be a differentiable shiftscale invariant function Then f... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Accounting Questions!

If y = f(u) and u = g(x), where f and are twice differentiable functions, show that d'y ( du dy d'u du dx d'y du? dx

There exists a function f such that f (1) = 2, f(3) = 0, and f(x) > 1 for all x.

There exists a function f such that f(x) > 0, f(x) 0 for all x.

Prove that the function defined by the equations \[ f(t)=f(-t), \quad f(t+2 a)=f(t), \quad f(t)=\frac{a-t}{a} \text { for } 0 \leqslant t \leqslant a \] is a characteristic function. The...

Answer the following 1. Solow model in continuous time. Consider the Solow model in continuous time with pro- duction function y = f(k) satisfying the usual properties, constant savings rate s,...

Solve the following questions 2. Consider a Cobb-Douglas Production function: f(I) = 1412, a >0, 8>0. (i) Sketch the production possibility set Z in each of the three cases; 1. a+ 8 1; 3. at3 =1. For...

=+12.10. Of minor interest is the k-dimensional analogue of (12.4). Let I, be (0, 1] for 1 20 and (1, 0] for 1 0, and let A, = / ,, x . .. x/, . Let (x) be +1 or -1 according as the number of i, 1...

Two-sided t-test. (i) Let X1,..., Xn be a sample from N(, 2). For testing = 0 against = 0, there exists a UMP invariant test with respect to the group X i = cXi , c = 0, given by the two-sided...

Solution Suppose f x f x Note that if x is odd and x is even then we will have x 1 x 1 i e x x 2 which is impossible Similarly the possibility of x being even and x being odd can also be ruled out...

(i) Let X be the totality of points x = (x1,...,xn) for which all coordinates are different from zero, and let G be the group of transformations x i = cxi,c > 0. Then a maximal invariant under G is...

Explain benchmarking.

Describe responsibility accounting Question 1 options: a) Without some form of responsibility accounting, there would be chaos in discharging management's control function. b) Costs and revenues can...

Unit 3 : Discussion Financial Statments Introduction In this LearnScape, the student is asked to assume the role of an experienced labor law attorney who recently joined the Board of Directors of...

The following is a draft set of simplified financial statements for Pear Limited for the year ended 30 September 2015.Income statement for the year ended 30 September 2015 Statement of financial...

You are comparing two companies in the same industry. You have determined that Lam Ltd. depreciates its plant assets over a 40-year life, whereas Shuey Ltd. depreciates its plant assets over a...

The students decided to compare the average ratings of the cafeteria food on the two scales. a. Find the mean and standard deviation of the ratings for the students who were given the 1-to-5 scale....

Shanahan Construction Company has entered into a contract beginning January 1, 2022, to build a parking complex. It has been estimated that the complex will cost $600,000 and will take 3 years to...

The currents iLa (t) and iC (t) of the inductor and capacitor in the circuit shown can be drawn as phasors in a phasor diagram. Use a phasor diagram to show that iL(t) + iC (t) = iS(t). i 1 c(t) 10 mH

a taxpayer may be exempt from early withdrawal penalty on all distributions since they were seperated from their emplyer after age 55

1. A function f (x) is graphed to the right; answer the following questions for this function. [Each 1] mi Jump discontinuity at x = n} Removable discontinuity at x = a) How the discontinuities are...

1 1 Consider function f (x) = ; xz. Find the absolute maximum and absolute minimum of f (x) on E, 00)

3G 4G 10:12 0 0 0.00 2: 41% Document View .. . Senior High School Basic Calculus Quarter 3 - Module 2: Limit Laws ADM ALE NMENT PROPERTY OT FOR S VERN GOVE Basic Calculus - Grade 11 Alternative...

subscribers to an online fash 37. foll magazine. Due to competition from an 8-month-old competing magazine 38. The constant function g (x) = 5e" is an anti number C(t) of subscribers is expected to...

1. Which of the following corresponds to the derivative of f (x) = 7 ng at x = 2, using the primary definition of a derivative, reduced to its simplest form before taking the limit? O A. f' (2) = lim...

Which of the following corresponds to the derivative of f (@) = , at x = 2, using the primary definition of a derivative, reduced to its simplest form before taking the limit? O A. f' (2) = lim -1 h...