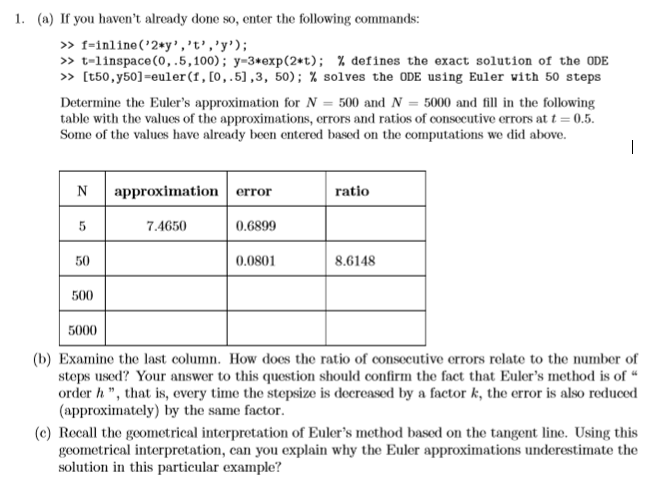
1. (a) If you haven't already done so, enter the following commands: f-inline ('2*y', 't' .'y); >> t-1 inspace(0, .5,100); y-3*exp(2*t); % defines the exact solution of the ODE >> [t50 , y50]-euler(, [0,.5] ,3, 50); % solves the ODE using Euler with 50 steps Determine the Euler's approximation for N 500 and N 5000 and fill in the following table with the values of the approximations, crrors and ratios of consecutive crrors at t-0.5 Some of the values have already been entered based on the computations we did above. Napproximation error 0.6899 0.0801 ratio 7.4650 50 500 5000 8.6148 (b) Examine the last column. How does the ratio of consccutive errors relate to the number of steps used? Your answer to this question should confirm the fact that Euler's method is of " order, that is, every time the stepsize is decreased by a factor k, the error is also reduced (approximately) by the same factor. (c) Recall the geometrical iterpretation of Euler's method based on the tangent line. Using this geometrical interpretation, can you explain why the Euler approximations underestimate the solution in this particular example? 1. (a) If you haven't already done so, enter the following commands: f-inline ('2*y', 't' .'y); >> t-1 inspace(0, .5,100); y-3*exp(2*t); % defines the exact solution of the ODE >> [t50 , y50]-euler(, [0,.5] ,3, 50); % solves the ODE using Euler with 50 steps Determine the Euler's approximation for N 500 and N 5000 and fill in the following table with the values of the approximations, crrors and ratios of consecutive crrors at t-0.5 Some of the values have already been entered based on the computations we did above. Napproximation error 0.6899 0.0801 ratio 7.4650 50 500 5000 8.6148 (b) Examine the last column. How does the ratio of consccutive errors relate to the number of steps used? Your answer to this question should confirm the fact that Euler's method is of " order, that is, every time the stepsize is decreased by a factor k, the error is also reduced (approximately) by the same factor. (c) Recall the geometrical iterpretation of Euler's method based on the tangent line. Using this geometrical interpretation, can you explain why the Euler approximations underestimate the solution in this particular example