1.
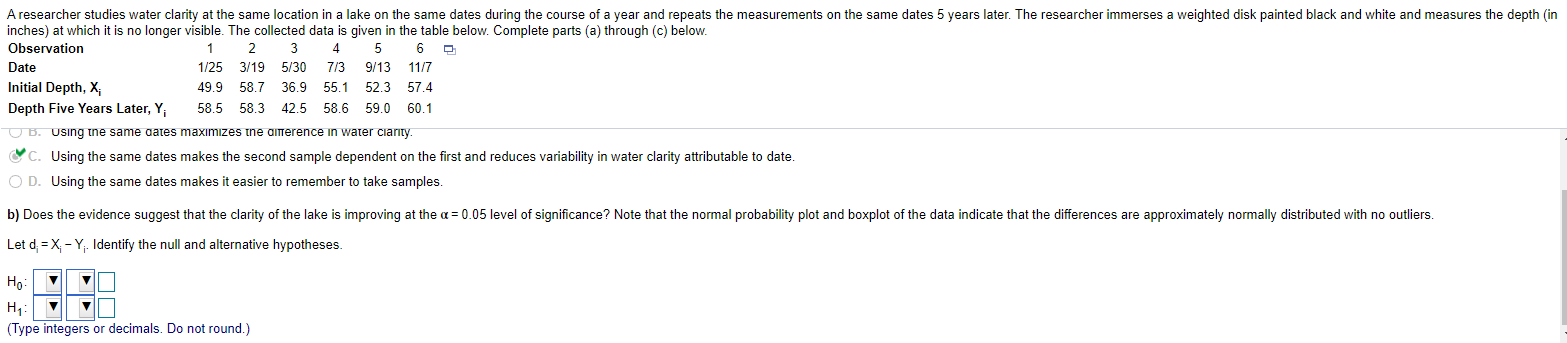
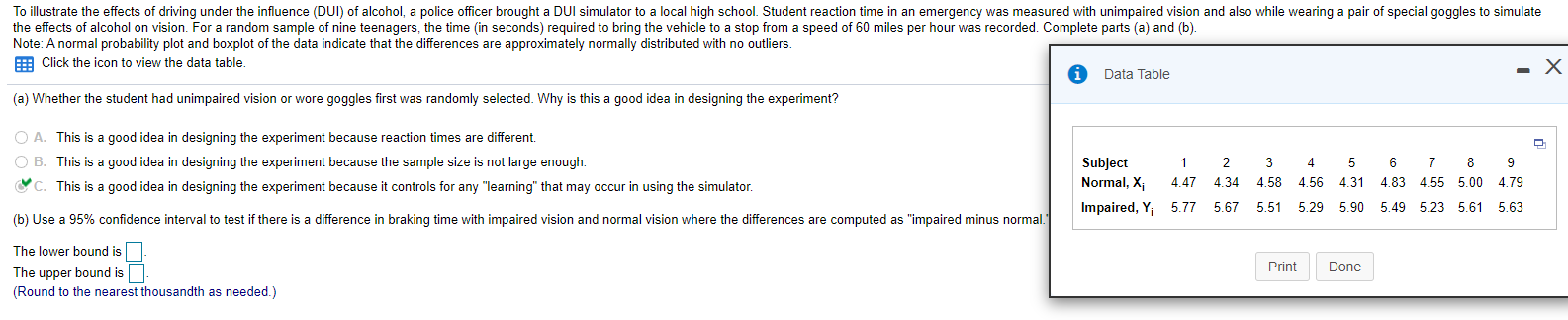
A researcher studies water clarity at the same location in a lake on the same dates during the course of a year and repeats the measurements on the same dates 5 years later. The researcher immerses a weighted disk painted black and white and measures the depth (in inches) at which it is no longer visible. The collected data is given in the table below. Complete parts (a) through (c) below. Observation 2 3 5 6 Date 1/25 3/19 5/30 7/3 9/13 11/7 Initial Depth, X; 49.9 58.7 36.9 55.1 52.3 57.4 Depth Five Years Later, Y; 5 58.3 42.5 58.6 59.0 60.1 O B. Using the same dates maximizes the difference in water clarity. C C. Using the same dates makes the second sample dependent on the first and reduces variability in water clarity attributable to date. O D. Using the same dates makes it easier to remember to take samples. b) Does the evidence suggest that the clarity of the lake is improving at the o= 0.05 level of significance? Note that the normal probability plot and boxplot of the data indicate that the differences are approximately normally distributed with no outliers. Let d; = X; - Y; Identify the null and alternative hypotheses. Ho H1 : (Type integers or decimals. Do not round.)\fAssume that the differences are normally distributed. Complete parts (a) through (d) below. Observation 1 2 3 4 5 6 7 8 :11 xi 43.6 53.5 49.4 43.9 44.8 52.6 46.0 45.3 Yi 48.2 52.9 52.3 48.8 45.6 52.4 46.1 45.1 (a) Determine di = Xi Yi for each pair of data. Observation 1 2 3 4 5 6 7 8 d: -4.6 0.6 -2.9 -4.9 0.8 0.2 -2.1 0.2 (Type integers or decimals.) (b) Compute d and 3d- d = - 1.788 (Round to three decimal places as needed.) 3d = 2.159 (Round to three decimal places as needed.) The manufacturer of hardness testing equipment uses steel-ball indenters to penetrate metal that is being tested. However, the manufacturer thinks it would be better to use a diamond indenter so that all types of metal can be tested. Because of differences between the two types of indenters, it is suspected that the two methods will produce different hardness readings. The metal specimens to be tested are large enough so that two indentions can be made. Therefore, the manufacturer uses both indenters on each specimen and compares the hardness readings. Construct a 95% confidence interval to judge whether the two indenters result in different measurements. X Note: A normal probability plot and boxplot of the data indicate that the differences are approximately normally distributed with no outliers. i Data Table Click the icon to view the data table. Construct a 95% confidence interval to judge whether the two indenters result in different measurements, where the differences are computed as 'diamond minus steel ball'. The lower bound is - 0.281 Specimen 1 2 3 4 5 6 7 8 9 The upper bound is - 3.052 Steel ball 51 57 61 71 68 54 65 51 53 (Round to the nearest tenth as needed.) Diamond 53 55 63 74 69 55 68 51 56To illustrate the effects of driving under the influence (DUI) of alcohol, a police officer brought a DUI simulator to a local high school. Student reaction time in an emergency was measured with unimpaired vision and also while wearing a pair of special goggles to simulate the effects of alcohol on vision. For a random sample of nine teenagers, the time (in seconds) required to bring the vehicle to a stop from a speed of 60 miles per hour was recorded. Complete parts (a) and (b). Note: A normal probability plot and boxplot of the data indicate that the differences are approximately normally distributed with no outliers. If Click the icon to view the data table. Data Table - X (a) Whether the student had unimpaired vision or wore goggles first was randomly selected. Why is this a good idea in designing the experiment? O A. This is a good idea in designing the experiment because reaction times are different. O B. This is a good idea in designing the experiment because the sample size is not large enough. Subject 2 3 4 5 6 7 8 9 C. This is a good idea in designing the experiment because it controls for any "learning" that may occur in using the simulator. Normal, X; 4.47 4.34 4.58 4.56 4.31 4.83 4.55 5.00 4.79 Impaired, Y; 5.77 5.67 5.51 5.29 5.90 5.49 5.23 5.61 5.63 (b) Use a 95% confidence interval to test if there is a difference in braking time with impaired vision and normal vision where the differences are computed as "impaired minus normal. The lower bound is The upper bound is Print Done (Round to the nearest thousandth as needed.)