1. Can you write the algorithmic form for the above description?

example:

 

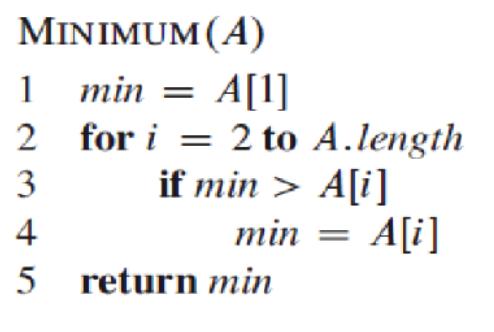
2. Show that your algorithm needs at most 3*n/2.

In fact, we can find both the minimum and the maximum using at most 3 [n/2] comparisons. We do so by maintaining both the minimum and maximum elements seen thus far. Rather than processing each element of the input by comparing it against the current minimum and maximum, at a cost of 2 comparisons per element, 9.2 Selection in expected linear time 215 we process elements in pairs. We compare pairs of elements from the input first with each other, and then we compare the smaller with the current minimum and the larger to the current maximum, at a cost of 3 comparisons for every 2 elements. How we set up initial values for the current minimum and maximum depends on whether n is odd or even. If n is odd, we set both the minimum and maximum to the value of the first element, and then we process the rest of the elements in pairs. If n is even, we perform 1 comparison on the first 2 elements to determine the initial values of the minimum and maximum, and then process the rest of the elements in pairs as in the case for odd n. Let us analyze the total number of comparisons. If n is odd, then we perform 3 [n/2] comparisons. If n is even, we perform 1 initial comparison followed by 3(n 2)/2 comparisons, for a total of 3n/2-2. Thus, in either case, the total number of comparisons is at most 3 [n/2].