Question
1. Compute running time of the following piece of code. For convenience the lines are numbered. Use cost and times columns to compute the running
1. Compute running time of the following piece of code. For convenience the lines are numbered. Use cost and times columns to compute the running time. (Cost of a line is the amount of time that is required to execute the line, e.g. constant c1. Times is the number of times the line is executed.) After you get the exact expression for the running time, represent it in big-Oh notation (O-notation).
1. int maxSum = 0;
2. for( int i = 0; i
3. int thisSum = 0;
4. for( int j = i; j 5. thisSum += a[j]; 6. if( thisSum > maxSum ) 7. maxSum = thisSum; } } 2. Explain clearly why the statement The running time of algorithm A is at least O(n2) does not make sense. 3. a) Let f(n) = 6n2 - 100n + 44 and g(n) = 0.5n3 . Prove that f(n) = O(g(n)) using the definition of Big-O notation. (You need to find constants c and n0). b) Let f(n) = 3n2 + n and g(n) = 2n2 . Use the definition of big-O notation to prove that f(n) = O(g(n)) (you need to find constants c and n0) and g(n) = O(f(n)) (you need to find constants c and n0). Conclude that f(n) = (g(n)). 4. Order the following 16 functions by asymptotic growth rate from lowest to highest. If any are of the same order then circle them on your list. 5n-6, 3, 5n+n3, 5. The purpose of this exercise is for you to experience a difference between exponential and polynomial algorithms. a) Implement the exponential algorithm to determine nth Fibonacci number from page 3 of the textbook. Implement the polynomial algorithm to determine nth Fibonacci number from page 4 of the textbook. Write a program that would compute execution time (as measured by the system clock) of each of the two algorithms for various values of n. b) Report obtained execution times of the two algorithms for different values of n (at least 10 different values). Your goal is to demonstrate the difference in execution times of the algorithms when n grows. Write obtained execution times in a table like the following: c) Experiment with your program or write another program to answer the following questions. What is the largest value of n for which nth Fibonacci number can be computed in less than 10 milliseconds by the exponential algorithm? What is the largest value of n for which nth Fibonacci number can be computed in less than 10 milliseconds by the polynomial algorithm?
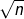 , n2.01, 3log2n, 4log n, n!, log n3, n1/3, 3n3-5n+n4, n log n +4n, 10n4, 4n, 2n, 4n+1. Note: When comparing two functions f(n) and g(n) you may use
, n2.01, 3log2n, 4log n, n!, log n3, n1/3, 3n3-5n+n4, n log n +4n, 10n4, 4n, 2n, 4n+1. Note: When comparing two functions f(n) and g(n) you may use 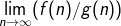 to compare their asymptotic growth rates.
to compare their asymptotic growth rates.
n Exponential Algorithm Polynomial Algorithm
Step by Step Solution
There are 3 Steps involved in it
Step: 1

Get Instant Access to Expert-Tailored Solutions
See step-by-step solutions with expert insights and AI powered tools for academic success
Step: 2

Step: 3

Ace Your Homework with AI
Get the answers you need in no time with our AI-driven, step-by-step assistance
Get Started


