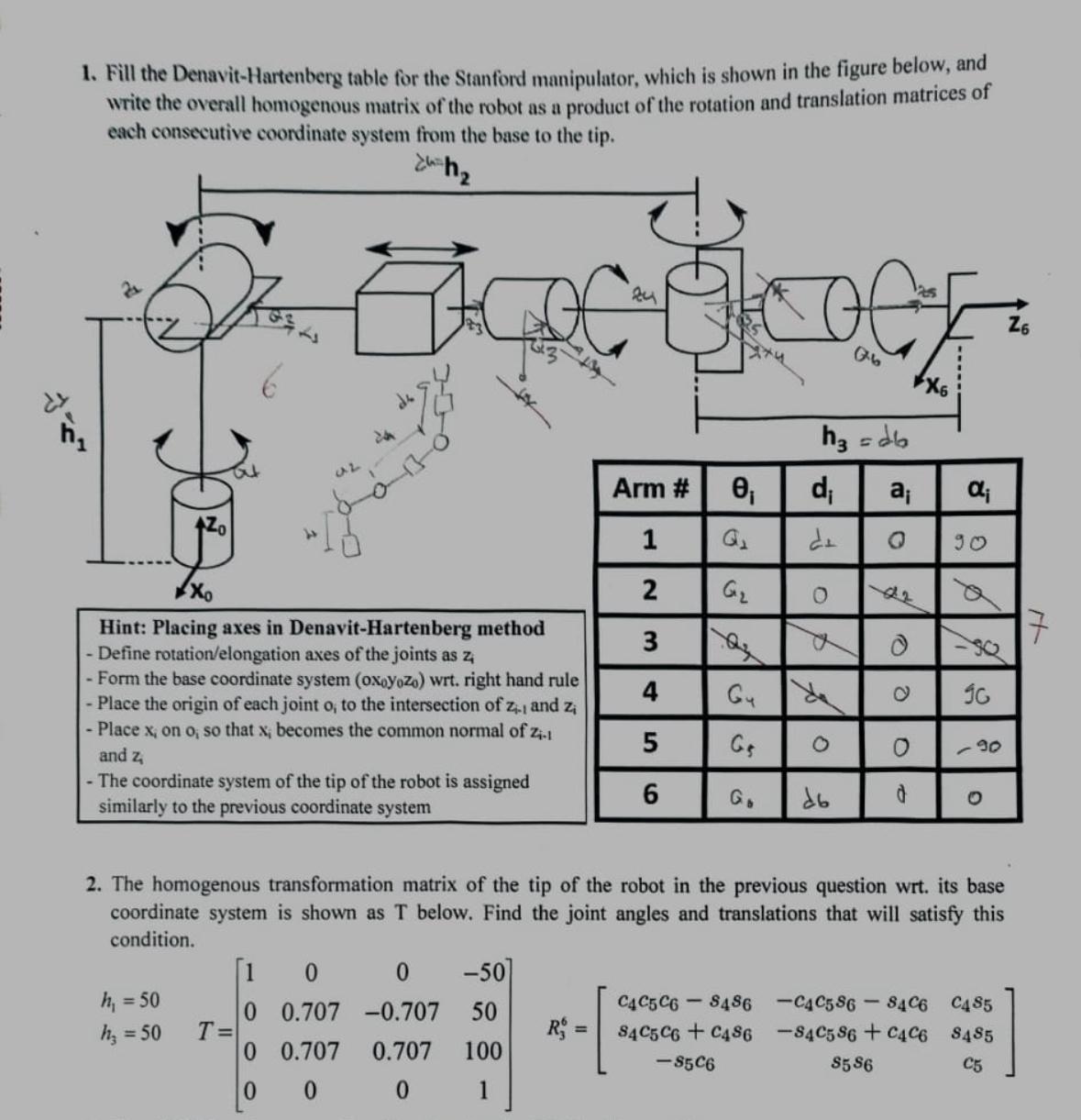
1. Fill the Denavit-Hartenberg table for the Stanford manipulator, which is shown in the figure below, and write the overall homogenous matrix of the robot as a product of the rotation and translation matrices of each consecutive coordinate system from the base to the tip. =h at Hint: Placing axes in Denavit-Hartenberg method - Define rotation/elongation axes of the joints as z 0 - Form the base coordinate system (oxoyozo) wrt. right hand rule - Place the origin of each joint o, to the intersection of z., and zi - Place x, on o, so that x; becomes the common normal of Zi-1 and z - The coordinate system of the tip of the robot is assigned similarly to the previous coordinate system h = 50 h = 50 T= 1 0 0 0.707 0 0.707 0 0 0 -50 -0.707 50 0.707 100 0 1 ty R = Arm # 1 2 3 4 5 6 C4 C5 C6 84 C5 C6 0 Q G -85C6 Gu G 8486 C486 h = db d de O a f O 76 d6 a; Q 2. The homogenous transformation matrix of the tip of the robot in the previous question wrt. its base coordinate system is shown as T below. Find the joint angles and translations that will satisfy this condition. ee O d 25 ; 90 96 -90 -C4C586-84C6 C4S85 -84C586 + C4C6 8485 $586 C5 Z6 17