(1))For these following coding problems, use the BinarySearchTree class that we used in lecture (code as a starting point. (See attachment files in eLearn assignment 9)

Write a method findHeight() that returns the height of the calling tree. Remember that the height is the maximum level of the tree, with level 1 being the root. (Hint: A recursive solution is nice and short.)

In class we discussed pre-order, in-order, and post-order traversals. Another common type of tree traversal is a level-order traversal. This involves visiting the nodes of the tree left-to-right, top-to-bottom (just like the way you normally read a page of text). For example, consider the BST below:

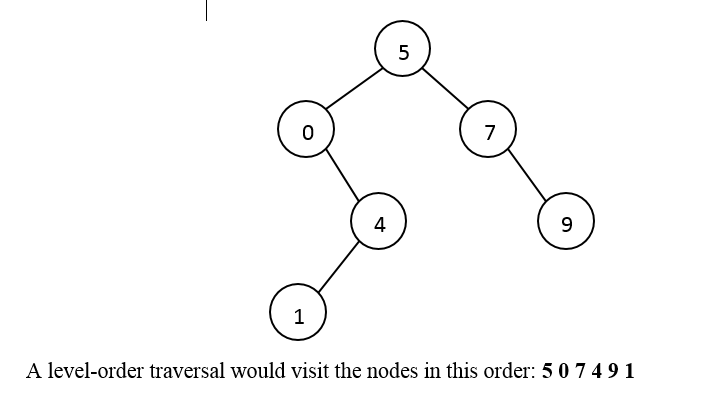
Write a levelOrderTraversal method. The method should print the nodes in the order that they are visited. (Hint: one non-recursive algorithm for this is to use a queue to keep track of the nodes that you want to visit. Start by enqueuing the root node, and see what needs to be done from there.)

files in eLearn assignment 9:

import java.util.Iterator;

import java.util.LinkedList;

import java.util.Queue;

import java.util.Stack;

/*

* This class implements a binary search tree.

*/

// The > means that whatever type we store in the tree

// must be from a class that implements the Comparable interface (i.e., provides

// a definition for the compareTo method).

//

// Any class that provides an iterator() method can implement the Iterable

// interface. This allows us to use the enhanced for syntax with objects of this class.

public class BinarySearchTree> implements Iterable {

// This nested class implements an in-order iterator over the elements of this BST

// (i.e., the elements are returned in the same order as an in-order traversal).

private class InOrderIterator implements Iterator { // Since InOrderIterator is not static, it *does* have access to the instance variables of BST.

private Node current = root;

private Stack> pile = new Stack();

@Override

public boolean hasNext() {

return !(current == null && pile.empty());

}

@Override

public E next() {

while (current != null) {

pile.push(current);

current = current.left;

}

Node popped = pile.pop();

current = popped.right;

return popped.data;

}

}

// This nested Node class is very similar to the one we used for

// LinkedList. But, tree nodes must keep track of both left

// and right children, instead of just one next node.

private static class Node { // "static" means that Node does *not* have access to the instance variables of BinarySearchTree

private E data;

private Node left, right;

// Constructor

public Node(E data, Node left, Node right) {

this.data = data;

this.left = left;

this.right = right;

}

}

private Node root;

/****** BEGIN HW 8 METHODS ******/

/****** All remaining methods were provided in lecture ******/

// Returns an in-order iterator over the elements of this BST.

public Iterator iterator() {

return new InOrderIterator();

}

// Wrapper method for preOrderTraversal

public void preOrderTraversal() {

System.out.println("Doing a pre-order traversal");

preOrderTraversal(root);

}

// Performs an pre-order traversal of the subtree rooted at where

private void preOrderTraversal(Node where) {

if (where != null) {

System.out.println(where.data);

preOrderTraversal(where.left);

preOrderTraversal(where.right);

}

}

// Wrapper method for inOrderTraversal

public void inOrderTraversal() {

System.out.println("Doing a in-order traversal");

inOrderTraversal(root);

}

// Performs an in-order traversal of the subtree rooted at where

private void inOrderTraversal(Node where) {

if (where != null) {

inOrderTraversal(where.left);

System.out.println(where.data);

inOrderTraversal(where.right);

}

}

// Wrapper method for postOrderTraversal

public void postOrderTraversal() {

System.out.println("Doing a post-order traversal");

postOrderTraversal(root);

}

// Performs a post-order traversal of the subtree rooted at where

private void postOrderTraversal(Node where) {

if (where != null) {

postOrderTraversal(where.left);

postOrderTraversal(where.right);

System.out.println(where.data);

}

}

// Wrapper method for find

public E find(E dataToFind) {

return find(dataToFind, root);

}

// Recursively finds dataToFind in the subtree rooted at where.

// Returns the item from the tree if found, or null if not found.

private E find(E dataToFind, Node where) {

if (where == null) // Empty subtree - dataToFind does not exist

return null;

else if (where.data.equals(dataToFind)) // dataToFind has been found

return where.data;

else {

// Determine whether to search the left or the right subtree

int compare = dataToFind.compareTo(where.data);

if (compare

return find(dataToFind, where.left);

else

return find(dataToFind, where.right);

}

}

// Wrapper method for add

public void add(E dataToAdd) {

root = add(dataToAdd, root);

}

// Recursively adds the dataToAdd to the subtree rooted at where.

// Returns a reference to where, with the dataToAdd already added.

private Node add(E dataToAdd, Node where) {

if (where == null) // We've reached an empty spot in the tree - dataToAdd should be added here!

return new Node(dataToAdd, null, null);

else {

// Determine whether to add to the left or right subtree

int compare = dataToAdd.compareTo(where.data);

if (compare

where.left = add(dataToAdd, where.left);

else if (compare > 0)

where.right = add(dataToAdd, where.right);

// Do nothing if compare == 0 (i.e., if dataToAdd already exists in the tree)

return where;

}

}

// Wrapper method for delete

public void delete(E dataToDelete) {

root = delete(dataToDelete, root);

}

// Recursively deletes dataToDelete from the subtree rooted at where.

// Returns a reference to where, with the dataToDelete already deleted.

private Node delete(E dataToDelete, Node where) {

if (where == null) // Empty subtree - nothing to delete

return null;

else {

// Determine whether to search down the left or right subtree

int compare = dataToDelete.compareTo(where.data);

if (compare

where.left = delete(dataToDelete, where.left);

return where;

} else if (compare > 0) {

where.right = delete(dataToDelete, where.right);

return where;

} else { // where contains dataToDelete

if (where.left == null && where.right == null) // Case 1: where has no children

return null;

else if (where.left != null && where.right == null) // Case 2a: where has only a left child

return where.left;

else if (where.left == null && where.right != null) // Case 2b: where has only a right child

return where.right;

else { // Case 3: where has 2 children, OH NOES run for the hills

where.data = findAndDeleteIOP(where);

return where;

}

}

}

}

// Finds and deletes the in-order predecessor of the node where.

// Returns the value of the IOP that was removed.

private E findAndDeleteIOP(Node where) {

// parent starts from where, temp starts from the root of where's left subtree

Node parent = where, temp = where.left;

// Move temp as far right as possible. When this loop exits,

// temp is pointing to where's in-order predecessor, and parent

// is pointing to the IOP's parent node.

while (temp.right != null) {

parent = temp;

temp = temp.right;

}

E toReturn = temp.data;

if (parent == where) // This means we have not moved down the tree at all - i.e., where's IOP is just where's left child

parent.left = temp.left;

else

parent.right = temp.left;

return toReturn;

}

// Wrapper method for toString (also overrides the toString inherited from Object)

public String toString() {

return toString(root, "");

}

// Recursively computes a toString of the subtree rooted at where.

// The indent parameter keeps track of how many spaces should be included in front.

private String toString(Node where, String indent) {

if (where == null)

return indent + "null";

else

return indent + where.data + " " + toString(where.left, indent + " ") + " " + toString(where.right, indent + " ");

}

public static void main(String[] args) {

BinarySearchTree myTree = new BinarySearchTree();

Integer[] data = {5, 8, 9, 10, 3, 0, -2};

for (Integer i : data)

myTree.add(i);

Iterator it = myTree.iterator();

while (it.hasNext())

System.out.println(it.next());

// Since BST implements Iterable, it can use the enhanced for syntax

// (which does the same thing as the iterator loop above)

for (Integer i : myTree)

System.out.println(i);

}

}

0 4 1 A level-order traversal would visit the nodes in this order: 507491