1. From the data for three conventional triaxial compression tests given below (confining pressure for first test: 4 Mpa; for second test: 7 MPa; for third test: 10 MPa):

a. Construct the failure envelope in principal stress (s₁-s₃) space. Find the failure parameters and the failure envelope equation.

b. Construct the Mohr-Coulomb failure envelope in s-t stress space. Find the failure parameters and the failure envelope equation.

c. Plot Youngs modulus, Bulk modulus, and shear modulus vs confining pressure

d. Plot Poissons ratio vs. confining pressure.

e. For the third confining pressure, acoustic velocities were recorded when the loading was at 50% of the failure. These velocities are: Vp = 3650 meters/sec; Vs = 2350 meters/sec. Find the ratio between Dynamic and Elastic Youngs moduli; Dynamic and Elastic Poissons ratios.

f. Construct the stress-strain relationship matrix {s}=[C]{e} and its inverse {e}=[X]{s} using equations 1.93 thru 1.98 and 1.102 thru 1.107 as given in the book by Fjaer et al, Rock Mechanics for Petroleum Engineers.

g. Using these relations, find the axial and radial strains in the sample for 80% of the failure stress of the 3^rd stage and using the E and n of the final stage. Compare the resulting strains with that of the graphs. Explain the difference, if it is there.

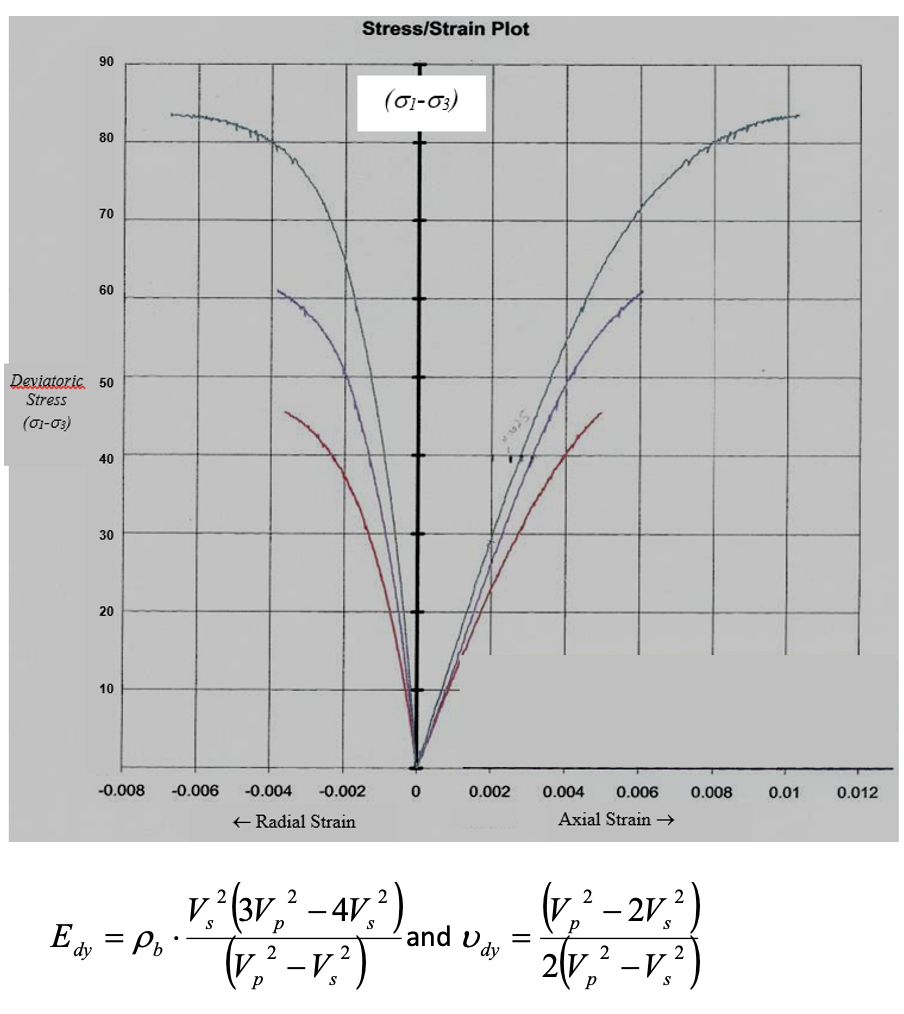
TIP: In order to avoid confusion regarding the units, use the following example for finding dynamic elastic moduli from velocities and density. Also note (1 Gpa = 145038 psi)

Given C_p = 20 MPa, V_p = 3298 m/s, V_s = 2153 m/s, E_st = 13.75 GPa and _st = 0.354 obtained from triaxial test.

Let us assume that _b=2.27 gm/cc [1gm/cc = 10³ Kg/m³]

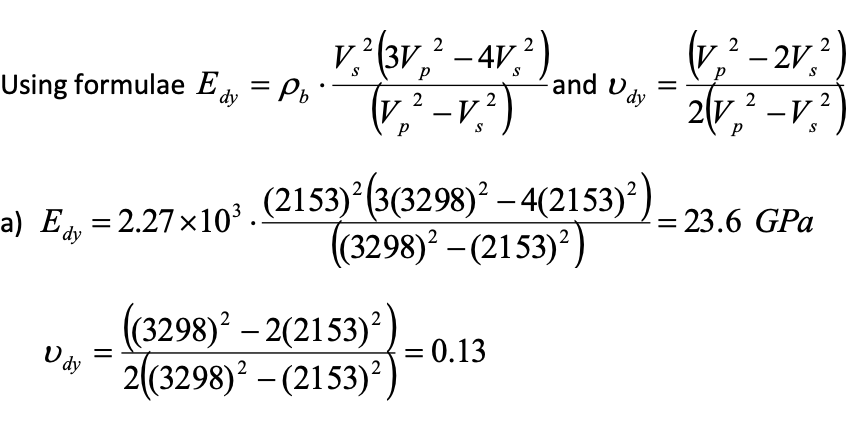
Edy = 23.6 Gpa = 23.6 *145038 psi = 3.42 million psi

Note that Young's modulus for A36 steel is 200 GPa (29 million psi) or almost 10 times this rocks value.

this how the question was posted

Stress/Strain Plot 90 (01-03) 80 70 60 Deviatoric 50 Stress (01-03) 40 30 20 10 -0.008 -0.006 -0.004 -0.002 0 0.002 0.004 0.006 0.008 0.01 0.012 + Radial Strain Axial Strain V,?(3V,? - 41,2) Edy = Pb. (V? - V.2) p care v- 2 2 and dy = (1,2-2v) 21V, -V,?) 2 p S 2 2 (v.2 - 2V , Using formulae Edy = Pb - and V dy = V o 1,2) 2\v2 -V2 . S V.?(3V,? - 41,2) 11,2 -1,2) -V a) E, = 2.27x103. (2153)| (3(3298)2 4(2153)). ((3298)2 (2153) _ ((3298) 2(2153) 2((3298)2 (2153) = = 23.6 GPa dy 2 - U dy = = 0.13 2 Stress/Strain Plot 90 (01-03) 80 70 60 Deviatoric 50 Stress (01-03) 40 30 20 10 -0.008 -0.006 -0.004 -0.002 0 0.002 0.004 0.006 0.008 0.01 0.012 + Radial Strain Axial Strain V,?(3V,? - 41,2) Edy = Pb. (V? - V.2) p care v- 2 2 and dy = (1,2-2v) 21V, -V,?) 2 p S 2 2 (v.2 - 2V , Using formulae Edy = Pb - and V dy = V o 1,2) 2\v2 -V2 . S V.?(3V,? - 41,2) 11,2 -1,2) -V a) E, = 2.27x103. (2153)| (3(3298)2 4(2153)). ((3298)2 (2153) _ ((3298) 2(2153) 2((3298)2 (2153) = = 23.6 GPa dy 2 - U dy = = 0.13 2