Question
1. Import the file ExperimentalData2.txt to your MATLAB folder. (I have the data so just ignore this step) The experimental data is two columns of
1. Import the file ExperimentalData2.txt to your MATLAB folder. (I have the data so just ignore this step)
The experimental data is two columns of numbers (for example: (first row) -1.51058, 0.230909).
2. Fit the experimental data to the function
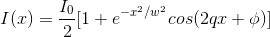 (1)
(1)
with fitting parameters I0, w, q and . Can you guess the value for I0 and ? Hint: Evaluate Eq. (1) at x = 0. Use your guessed values for I0 and as initial parameters. For w and q use 1 and 10, respectively.
3. Plot the experimental data and the fitted line in the same plot. Add position (mm) and intensity (a.u.) as your x and y axis labels. Do not forget a legend for your plot. (Just write the code on matlab as if you had the data, no need to run it to show me the graph because it wont work (as you probably know))
4. Does your fitted line look uneven? Try to plot your fitted line using more points to your independent variable. Hint: Define a new column vector with elements from -1.5 to 1.5 in steps of 0.01 and use it into the command predict. (Again just write the code)
5. The experimental data seems to have a Gaussian envelope. Plot that envelope in the same plot and report its full width at half maximum (FWHM). Add the corresponding label on the plot legend. Hint 1: What happens if you simply ignore the cosine function in Eq. (1) and plot the resulting expression? Hint 2: A general Gaussian function centered at x = 0 is given by
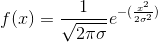 (2)
(2)
Where is the standard deviation. The FWHM for this Gaussian function is  (Same here)
(Same here)
Thank you for the help
Step by Step Solution
There are 3 Steps involved in it
Step: 1

Get Instant Access to Expert-Tailored Solutions
See step-by-step solutions with expert insights and AI powered tools for academic success
Step: 2

Step: 3

Ace Your Homework with AI
Get the answers you need in no time with our AI-driven, step-by-step assistance
Get Started


