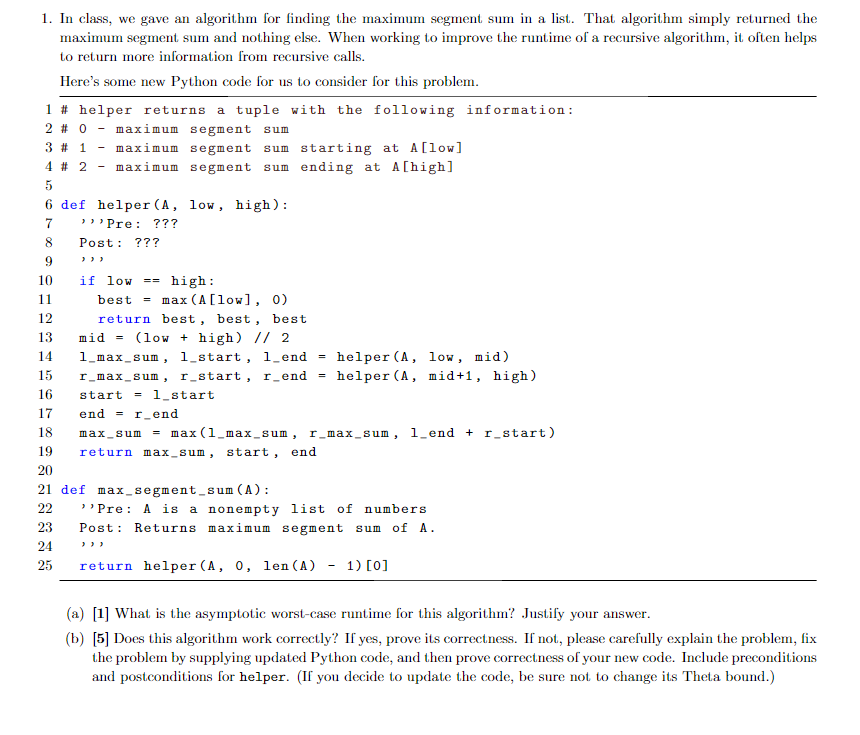
1. In class, we gave an algorithm for linding the maximum segment sum in a list. That algorithm simply returned the a recursive algorithm, it often helps maximum segment sum and nothing else. When working to improve the runtime of to return more information from recursive calls Here's some new Python code for us to consider for this problem 1 # helper returns a tuple with the following information: 2 # 0 - maximum segment sum 3 # 1 - maximum segment sum starting at A[low] 4 # 2 - maximum segment sum ending at A[high] 6 def helper (A, low, high): 7Pre ??? 8 Post ??? 9 10 if low - high: best = max (A [low], 0) 12 13 mid(low high) // 2 14 1-max-sun, 1-start, 1-end helper(A, low , mid) 15 r-max-sum, r-start, r-end = helper (A , mid+1, high) 16 start1 start 17 endr_end 18 max sum-max (1_max sum, r_max sum, l end + r start 19 return max_sum, start, end 20 21 def max_segment sum (A) 22 ,Pre: A is a nonempty list of numbers 23 Post: Returns maximum segment sum of A return best, best, best 25return helper (A, 0, len (A) -1) [0] (a) [1] What is the asymptotic worst-case runtime for this algorithm? Justify your answer (b) [5] Does this algorithm work correctly? I yes, prove its correctness. If not, please carefully explain the problem, fix the problem by supplying updated Python code, and then prove correctness of your new code. Include preconditions and postconditions for helper. (If you decide to update the code, be sure not to change its Theta bound.) 1. In class, we gave an algorithm for linding the maximum segment sum in a list. That algorithm simply returned the a recursive algorithm, it often helps maximum segment sum and nothing else. When working to improve the runtime of to return more information from recursive calls Here's some new Python code for us to consider for this problem 1 # helper returns a tuple with the following information: 2 # 0 - maximum segment sum 3 # 1 - maximum segment sum starting at A[low] 4 # 2 - maximum segment sum ending at A[high] 6 def helper (A, low, high): 7Pre ??? 8 Post ??? 9 10 if low - high: best = max (A [low], 0) 12 13 mid(low high) // 2 14 1-max-sun, 1-start, 1-end helper(A, low , mid) 15 r-max-sum, r-start, r-end = helper (A , mid+1, high) 16 start1 start 17 endr_end 18 max sum-max (1_max sum, r_max sum, l end + r start 19 return max_sum, start, end 20 21 def max_segment sum (A) 22 ,Pre: A is a nonempty list of numbers 23 Post: Returns maximum segment sum of A return best, best, best 25return helper (A, 0, len (A) -1) [0] (a) [1] What is the asymptotic worst-case runtime for this algorithm? Justify your answer (b) [5] Does this algorithm work correctly? I yes, prove its correctness. If not, please carefully explain the problem, fix the problem by supplying updated Python code, and then prove correctness of your new code. Include preconditions and postconditions for helper. (If you decide to update the code, be sure not to change its Theta bound.)







