
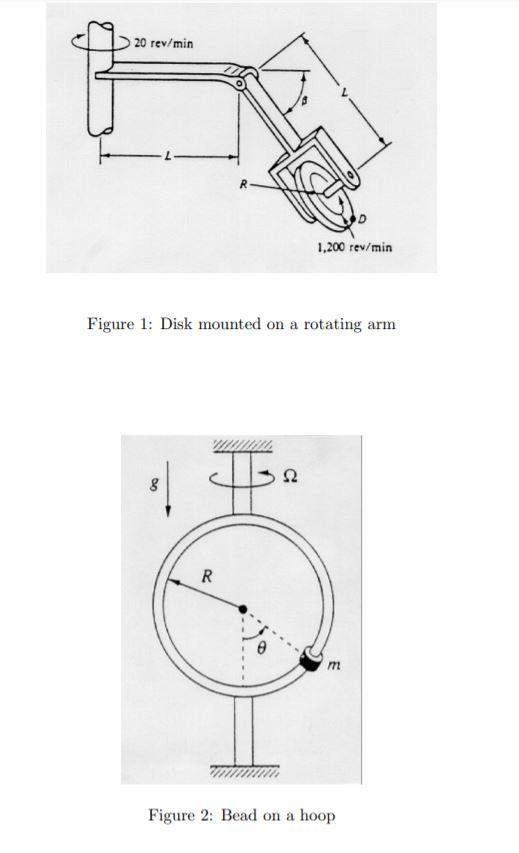
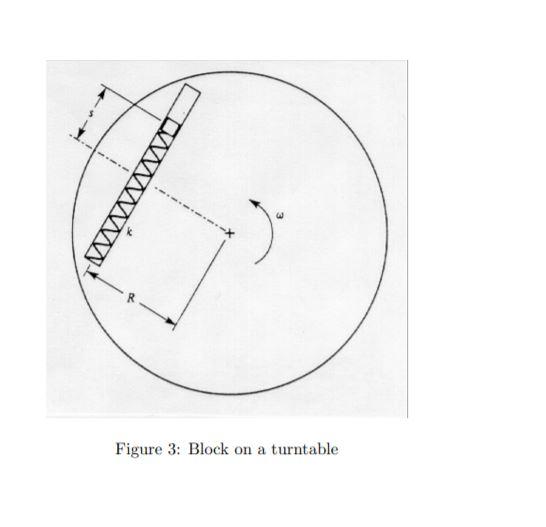
1. Inertial velocity and inertial acceleration (8 pts) The disk shown in Fig. 1 spins about its own central axis at 1200 rpm while the entire system rotates about the vertical axis (which is fixed in an inertial frame) at 20 rpm. The angle of inclination B is constant at 30 deg. Determine the inertial acceleration of point D on the perimeter of the disk when it is at its lowest position, as shown. For this problem, L = 1 m and R = 30 cm. 2. Equation of motion (8 pts) See Fig. 2. A bead (particle) of mass m is free to slide on a frictionless hoop of radius R. The hoops spins with respect to an inertial frame at a constant angular rate 1 about a vertical axis. Find the equation of motion for the bead. 3. Equation of motion and constraint force (8 pts) A small block (particle) of mass m slides within a smooth groove on a turntable (see Fig. 3). The block is connected to a spring of stiffness k which is unstressed when s = 0. The rotation rate of the turntable with respect to inertial space is a known function of time wit). (You may assume that the turntable is on a horizontal surface so that gravity is irrelevant.) Find the equation of motion for the block and the force exerted by the groove wall on the block. 20 rev/min 1,200 rev/min Figure 1: Disk mounted on a rotating arm 5 22 8 R m Figure 2: Bead on a hoop Figure 3: Block on a turntable 1. Inertial velocity and inertial acceleration (8 pts) The disk shown in Fig. 1 spins about its own central axis at 1200 rpm while the entire system rotates about the vertical axis (which is fixed in an inertial frame) at 20 rpm. The angle of inclination B is constant at 30 deg. Determine the inertial acceleration of point D on the perimeter of the disk when it is at its lowest position, as shown. For this problem, L = 1 m and R = 30 cm. 2. Equation of motion (8 pts) See Fig. 2. A bead (particle) of mass m is free to slide on a frictionless hoop of radius R. The hoops spins with respect to an inertial frame at a constant angular rate 1 about a vertical axis. Find the equation of motion for the bead. 3. Equation of motion and constraint force (8 pts) A small block (particle) of mass m slides within a smooth groove on a turntable (see Fig. 3). The block is connected to a spring of stiffness k which is unstressed when s = 0. The rotation rate of the turntable with respect to inertial space is a known function of time wit). (You may assume that the turntable is on a horizontal surface so that gravity is irrelevant.) Find the equation of motion for the block and the force exerted by the groove wall on the block. 20 rev/min 1,200 rev/min Figure 1: Disk mounted on a rotating arm 5 22 8 R m Figure 2: Bead on a hoop Figure 3: Block on a turntable









