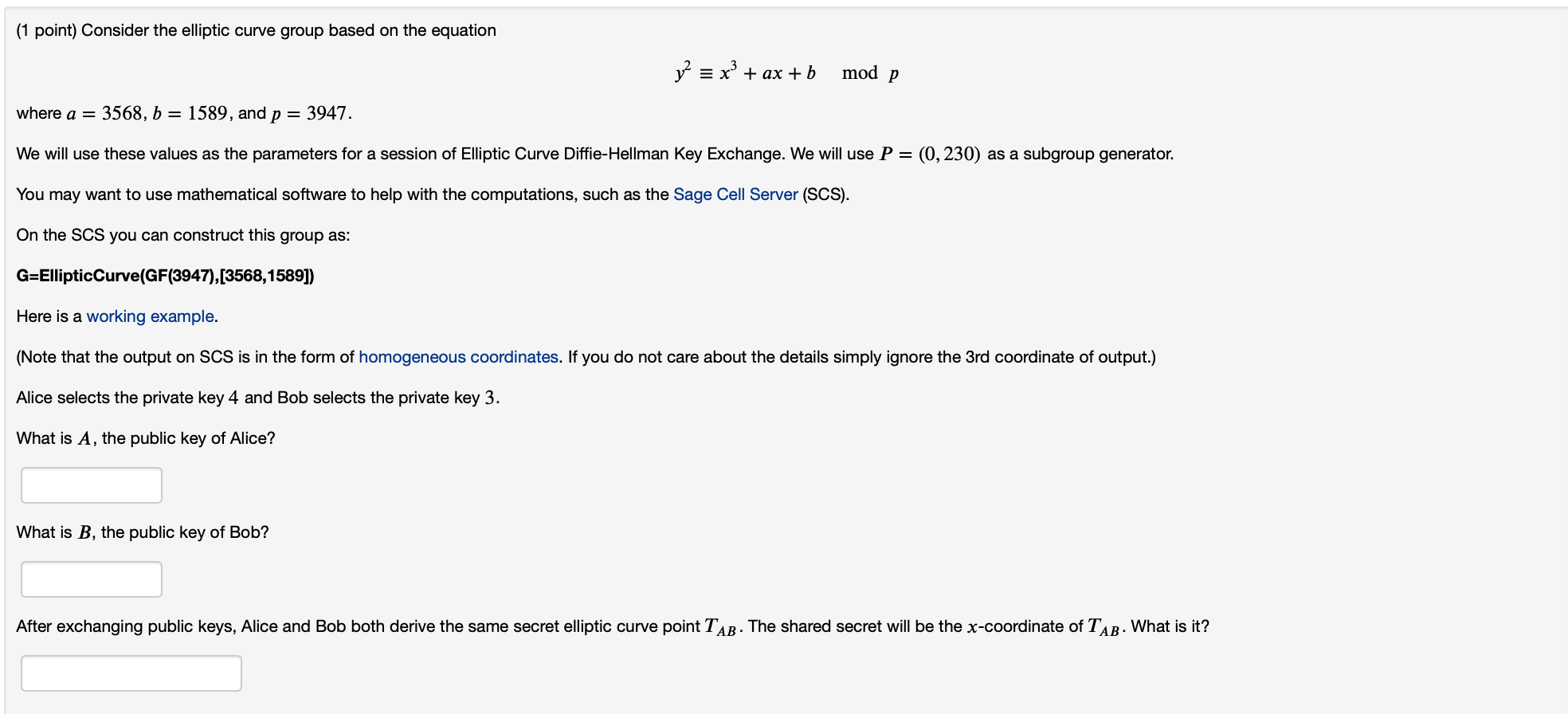
$(1$ point$)$ Consider the elliptic curve group based on the equation

$y^2-=x^3+ax+b,$modp

where $a=3568,b=1589,$ and $p=3947.$

We will use these values as the parameters for a session of Elliptic Curve Diffie$-$Hellman Key Exchange. We will use $P=(0,230)$ as a subgroup generator.

You may want to use mathematical software to help with the computations, such as the Sage Cell Server $($SCS$).$

On the SCS you can construct this group as:

G$=$EllipticCurve$($GF$(3947),[3568,1589])$

Here is a working example.

$($Note that the output on SCS is in the form of homogeneous coordinates. If you do not care about the details simply ignore the $3$rd coordinate of output.$)$

Alice selects the private key $4$ and Bob selects the private key $3.$

What is $A,$ the public key of Alice?

What is $B,$ the public key of Bob?

After exchanging public keys, Alice and Bob both derive the same secret elliptic curve point $T_{AB}.$ The shared secret will be the $x-$coordinate of $T_{AB}.$ What is it$?$