Answered step by step
Verified Expert Solution
Question
1 Approved Answer
(1 point) Determine which of the points (-1, 1, -5), (4, 7, -3), and (-9, 3, 2) lie in the plane X1 6x2 3x3
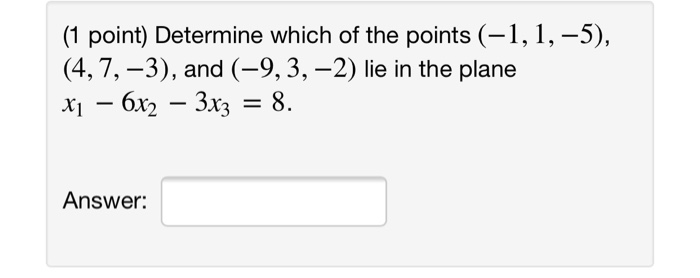

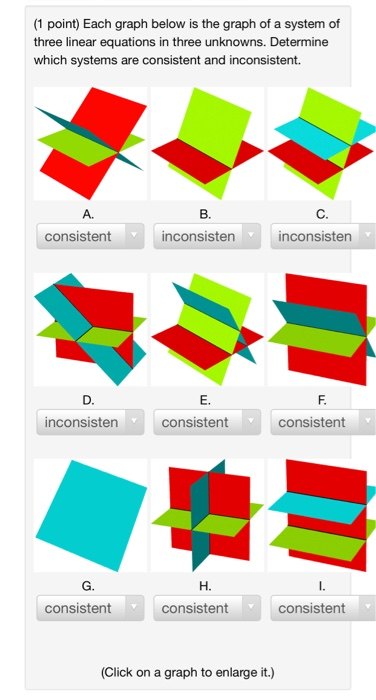

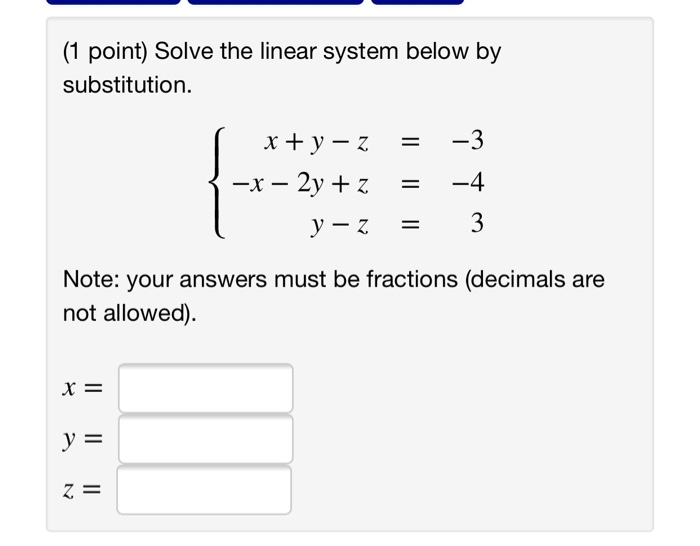

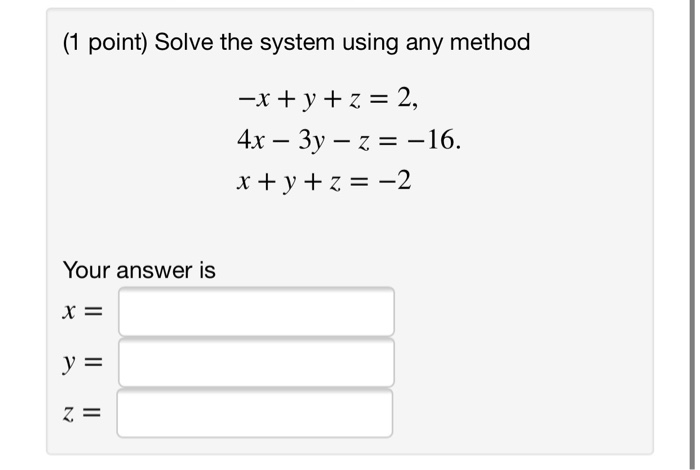

(1 point) Determine which of the points (-1, 1, -5), (4, 7, -3), and (-9, 3, 2) lie in the plane X1 6x2 3x3 = 8. Answer: (1 point) Determine which of the points (-4, -5, -6), (5, 6, 4), and (3, 4, 4) satisfy the linear system -3x1 + -6x1 Answer: 2x2 + 2x3 4x2 + 5x3 = -9 -54 (1 point) Each graph below is the graph of a system of three linear equations in three unknowns. Determine which systems are consistent and inconsistent. A. consistent D. inconsisten G. consistent B. inconsisten E. consistent H. consistent (Click on a graph to enlarge it.) C. inconsisten F. consistent consistent (1 point) Find the set of solutions for the linear system + 3x2 -9 3 -8 X1 - (X, X, X3) = - 3x3 - 2x3 2x3 Use s1, s2, etc. for the free variables if necessary. || " (1 point) Solve the linear system below by substitution. X = y = x+y=z -x - 2y + z y-z Note: your answers must be fractions (decimals are not allowed). Z = || -3 -4 3 (1 point) Solve the system using matrices (row operations) 4x -y +z = -16 -5x + 6y + 4z = 51 2x - 3y + 6z = 17 How many solutions are there to this system? A. None B. Exactly 1 C. Exactly 2 D. Exactly 3 E. Infinitely many F. None of the above If there is one solution, give its coordinates in the answer spaces below. If there are infinitely many solutions, enter z in the answer blank for z, enter a formula for y in terms of z in the answer blank for y and enter a formula for x in terms of z in the answer blank for .x. If there are no solutions, leave the answer blanks for x, y and z empty. X = y = Z= (1 point) Solve the system using any method -x + y + z = 2, 4x - 3y z = -16. x+y+z= -2 Your answer is X = y = Z = (1 point) Find the set of solutions for the linear system - 3x1 + 5x2 + 4x3 6x2 + 8x3 Use s1, s2, etc. for the free variables if necessary. (X1, X2, X3) " -9 7 (1 point) Determine which of the points (-1, 1, -5), (4, 7, -3), and (-9, 3, 2) lie in the plane X1 6x2 3x3 = 8. Answer: (1 point) Determine which of the points (-4, -5, -6), (5, 6, 4), and (3, 4, 4) satisfy the linear system -3x1 + -6x1 Answer: 2x2 + 2x3 4x2 + 5x3 = -9 -54 (1 point) Each graph below is the graph of a system of three linear equations in three unknowns. Determine which systems are consistent and inconsistent. A. consistent D. inconsisten G. consistent B. inconsisten E. consistent H. consistent (Click on a graph to enlarge it.) C. inconsisten F. consistent consistent (1 point) Find the set of solutions for the linear system + 3x2 -9 3 -8 X1 - (X, X, X3) = - 3x3 - 2x3 2x3 Use s1, s2, etc. for the free variables if necessary. || " (1 point) Solve the linear system below by substitution. X = y = x+y=z -x - 2y + z y-z Note: your answers must be fractions (decimals are not allowed). Z = || -3 -4 3 (1 point) Solve the system using matrices (row operations) 4x -y +z = -16 -5x + 6y + 4z = 51 2x - 3y + 6z = 17 How many solutions are there to this system? A. None B. Exactly 1 C. Exactly 2 D. Exactly 3 E. Infinitely many F. None of the above If there is one solution, give its coordinates in the answer spaces below. If there are infinitely many solutions, enter z in the answer blank for z, enter a formula for y in terms of z in the answer blank for y and enter a formula for x in terms of z in the answer blank for .x. If there are no solutions, leave the answer blanks for x, y and z empty. X = y = Z= (1 point) Solve the system using any method -x + y + z = 2, 4x - 3y z = -16. x+y+z= -2 Your answer is X = y = Z = (1 point) Find the set of solutions for the linear system - 3x1 + 5x2 + 4x3 6x2 + 8x3 Use s1, s2, etc. for the free variables if necessary. (X1, X2, X3) " -9 7 (1 point) Determine which of the points (-1, 1, -5), (4, 7, -3), and (-9, 3, 2) lie in the plane X1 6x2 3x3 = 8. Answer: (1 point) Determine which of the points (-4, -5, -6), (5, 6, 4), and (3, 4, 4) satisfy the linear system -3x1 + -6x1 Answer: 2x2 + 2x3 4x2 + 5x3 = -9 -54 (1 point) Each graph below is the graph of a system of three linear equations in three unknowns. Determine which systems are consistent and inconsistent. A. consistent D. inconsisten G. consistent B. inconsisten E. consistent H. consistent (Click on a graph to enlarge it.) C. inconsisten F. consistent consistent (1 point) Find the set of solutions for the linear system + 3x2 -9 3 -8 X1 - (X, X, X3) = - 3x3 - 2x3 2x3 Use s1, s2, etc. for the free variables if necessary. || " (1 point) Solve the linear system below by substitution. X = y = x+y=z -x - 2y + z y-z Note: your answers must be fractions (decimals are not allowed). Z = || -3 -4 3 (1 point) Solve the system using matrices (row operations) 4x -y +z = -16 -5x + 6y + 4z = 51 2x - 3y + 6z = 17 How many solutions are there to this system? A. None B. Exactly 1 C. Exactly 2 D. Exactly 3 E. Infinitely many F. None of the above If there is one solution, give its coordinates in the answer spaces below. If there are infinitely many solutions, enter z in the answer blank for z, enter a formula for y in terms of z in the answer blank for y and enter a formula for x in terms of z in the answer blank for .x. If there are no solutions, leave the answer blanks for x, y and z empty. X = y = Z= (1 point) Solve the system using any method -x + y + z = 2, 4x - 3y z = -16. x+y+z= -2 Your answer is X = y = Z = (1 point) Find the set of solutions for the linear system - 3x1 + 5x2 + 4x3 6x2 + 8x3 Use s1, s2, etc. for the free variables if necessary. (X1, X2, X3) " -9 7 (1 point) Determine which of the points (-1, 1, -5), (4, 7, -3), and (-9, 3, 2) lie in the plane X1 6x2 3x3 = 8. Answer: (1 point) Determine which of the points (-4, -5, -6), (5, 6, 4), and (3, 4, 4) satisfy the linear system -3x1 + -6x1 Answer: 2x2 + 2x3 4x2 + 5x3 = -9 -54 (1 point) Each graph below is the graph of a system of three linear equations in three unknowns. Determine which systems are consistent and inconsistent. A. consistent D. inconsisten G. consistent B. inconsisten E. consistent H. consistent (Click on a graph to enlarge it.) C. inconsisten F. consistent consistent (1 point) Find the set of solutions for the linear system + 3x2 -9 3 -8 X1 - (X, X, X3) = - 3x3 - 2x3 2x3 Use s1, s2, etc. for the free variables if necessary. || " (1 point) Solve the linear system below by substitution. X = y = x+y=z -x - 2y + z y-z Note: your answers must be fractions (decimals are not allowed). Z = || -3 -4 3 (1 point) Solve the system using matrices (row operations) 4x -y +z = -16 -5x + 6y + 4z = 51 2x - 3y + 6z = 17 How many solutions are there to this system? A. None B. Exactly 1 C. Exactly 2 D. Exactly 3 E. Infinitely many F. None of the above If there is one solution, give its coordinates in the answer spaces below. If there are infinitely many solutions, enter z in the answer blank for z, enter a formula for y in terms of z in the answer blank for y and enter a formula for x in terms of z in the answer blank for .x. If there are no solutions, leave the answer blanks for x, y and z empty. X = y = Z= (1 point) Solve the system using any method -x + y + z = 2, 4x - 3y z = -16. x+y+z= -2 Your answer is X = y = Z = (1 point) Find the set of solutions for the linear system - 3x1 + 5x2 + 4x3 6x2 + 8x3 Use s1, s2, etc. for the free variables if necessary. (X1, X2, X3) " -9 7
Step by Step Solution
★★★★★
3.30 Rating (168 Votes )
There are 3 Steps involved in it
Step: 1

Get Instant Access to Expert-Tailored Solutions
See step-by-step solutions with expert insights and AI powered tools for academic success
Step: 2

Step: 3

Ace Your Homework with AI
Get the answers you need in no time with our AI-driven, step-by-step assistance
Get Started


