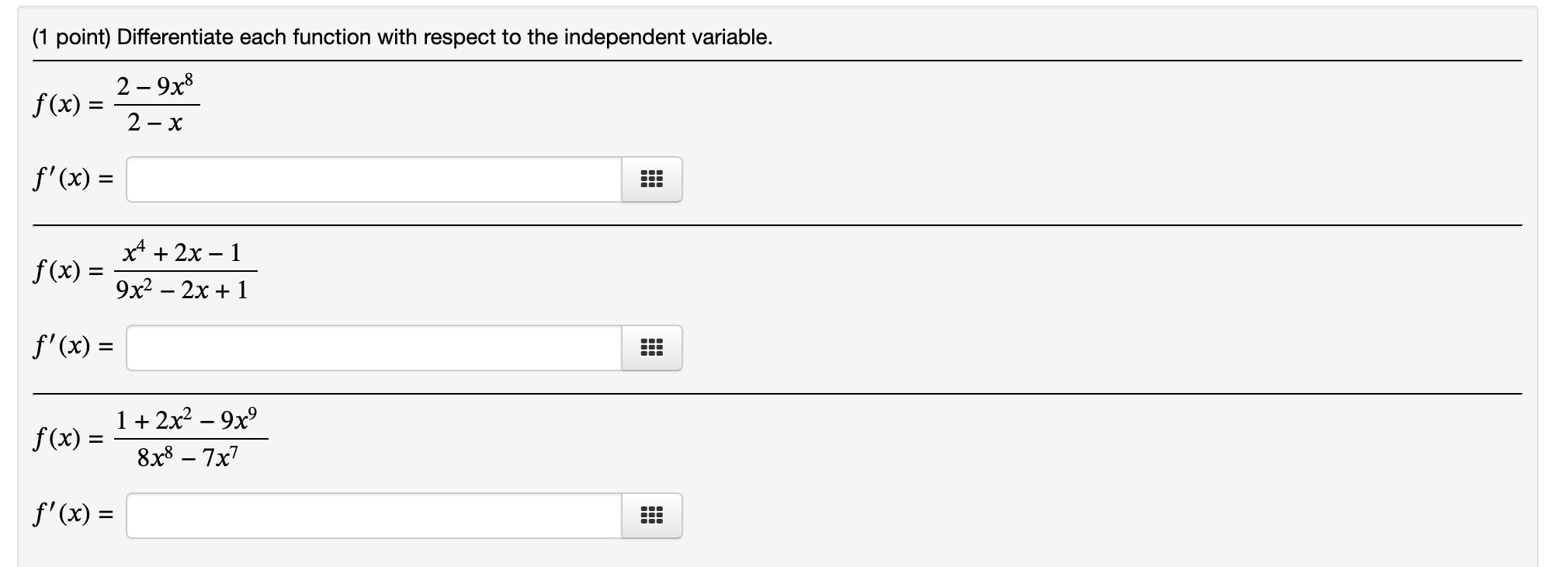
(1 point) Use the product rule to find an equation for the tangent line to y = f(x) at the indicated point. Solve your equation for y. f(x) = (87x)(8+7x), at x = 7 Tangent line is y = f(x) = (7x7 = 7)(8 - 8x), at x = 0 - Tangent line is y = (1 point) Apply the product rule repeatedly to find the derivative of y = f (x). f(x) = (x 6)(5 - 6x)(6 - x) f'(x) = f(x)=(5x+6)(7 - x)(6 + x) f'(x) = (1 point) Suppose that f(7) = 7,g(7) = 2, f' (7) = 3, and g (7) = 7. Find ( + g)'(7). ( + g)' (7) = (1 point) Consider the chemical reaction A + B AB. If x denotes the concentration of AB at time t, then the reaction rate R(x) is given by R(x) = k(ax)(b-x) where k, a, and b are positive constants. Differentiate R(x). R'(x) = (1 point) Find the derivative of y at x = 8, assuming that f(8) = 5 and f' (8) = 8. y = 6x f(x) y (8) = xf(x) y = 5 y(8)= (1 point) Differentiate each function with respect to the independent variable. 2-9x8 f(x) = 2- -x f'(x) = x+2x-1 f(x) = 9x - 2x+1 f'(x) = 1+2x - 9x9 f(x) = 8x8 - 7x7 f'(x)=