Question: (1 point) Your shady uncle has given you a six-sided die that he claims is weighted so that the six is 4 times as likely
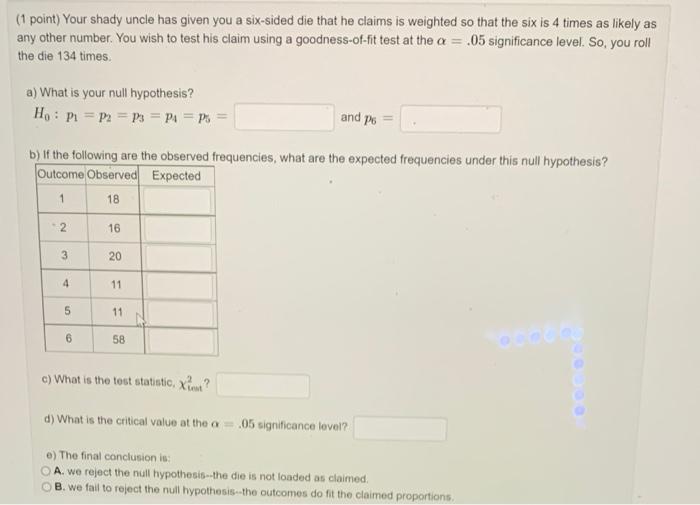
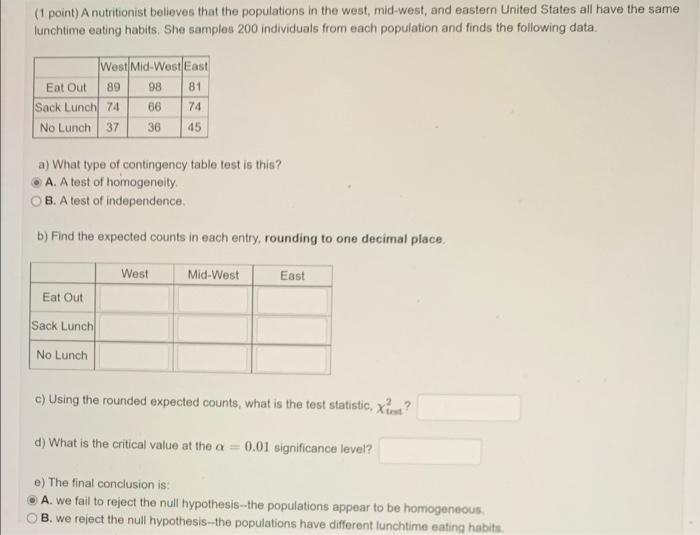

(1 point) Your shady uncle has given you a six-sided die that he claims is weighted so that the six is 4 times as likely as any other number. You wish to test his claim using a goodness-of-fit test at the a = .05 significance level. So, you roll the die 134 times a) What is your null hypothesis? H. : P1 = P2 = P3 = P4 = p = and po b) If the following are the observed frequencies, what are the expected frequencies under this null hypothesis? Outcome Observed Expected 1 18 2 16 3 20 4 11 5 11 6 58 c) What is the test statistic, Xi? d) What is the critical value at the o= .05 significance level? e) The final conclusion is: A. we reject the null hypothesis--the die is not loaded as claimed. B. we fail to reject the null hypothesis--the outcomes do fit the claimed proportions. (1 point) A nutritionist believes that the populations in the west, mid-west, and eastern United States all have the same lunchtime eating habits. She samples 200 individuals from each population and finds the following data. West Mid-West East Eat Out 89 98 81 Sack Lunch 74 66 74 No Lunch 37 36 45 a) What type of contingency table test is this? A. A test of homogeneity. 8. A test of independence. b) Find the expected counts in each entry, rounding to one decimal place. West Mid-West East Eat Out Sack Lunch No Lunch c) Using the rounded expected counts, what is the test statistic, xi? 2 d) What is the critical value at the a = 0.01 significance level? e) The final conclusion is: A. we fail to reject the null hypothesis--the populations appear to be homogeneous B. we reject the null hypothesis--the populations have different lunchtime eating habits. (1 point) it has been suggested that the highest priority of retirees is travel. Thus, a study was conducted to investigate the differences in the length of stay of a trip for pre- and post-retirees. A sample of 708 travelers were asked how long they stayed on a typical trip. The observed results of the study are found below. Number of Nights Pre-retirement Post-retirement Total 240 174 414 8 - 13 85 75 160 14 - 21 38 50 88 22 or more 16 30 46 Total 329 708 379 a) With this information, construct a table of estimated expected values. Number of Nights Pre-retirement Post-retirement 8-13 14-21 22 or more Now, with that information, determine whether the length of stay is independent of retirement using a = 0,05, b) The test statistic is x? c) The rejection region is x?> d) The final conclusion is
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


