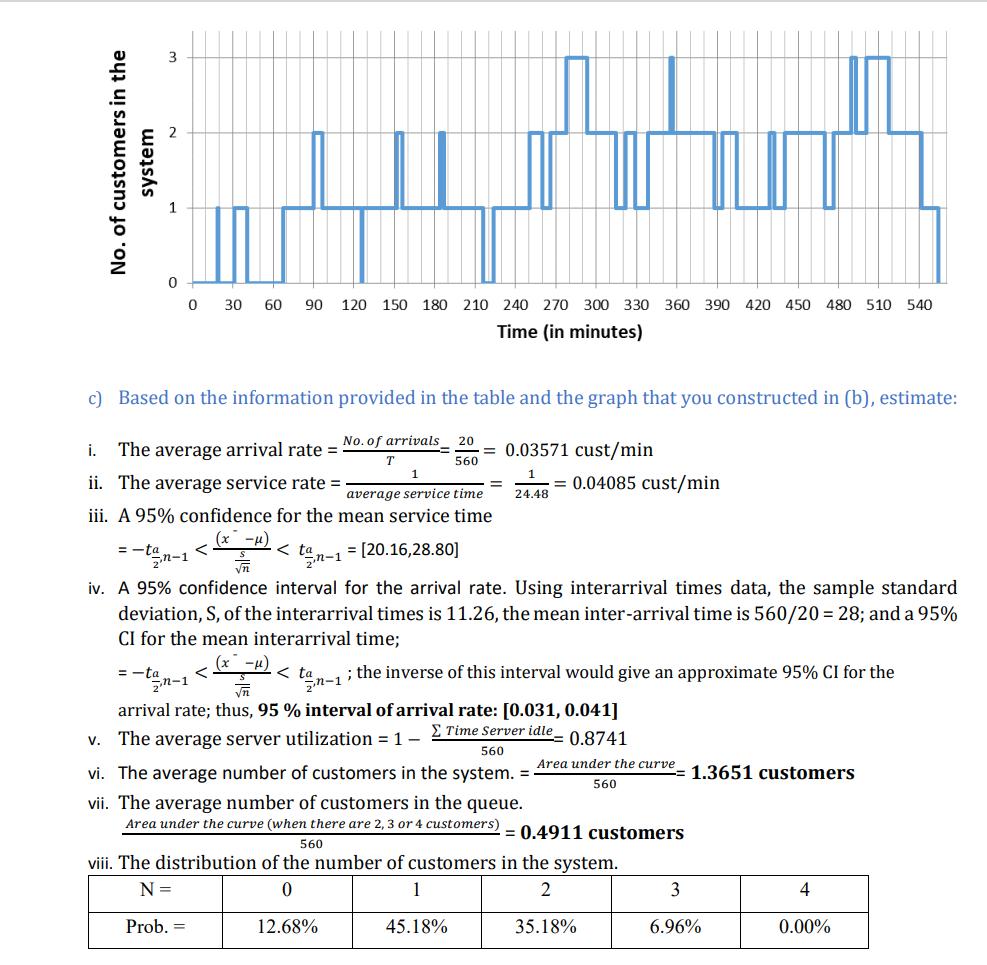
1) Suppose there is a service center consisting of a single server. Let the external arrival process be Poisson with rate , and the service times be exponential with mean service-time 1/. The interarrival times (time between arrivals) and the service times of 20 customers have been recorded and they are shown in the table below; the other columns in the table can be calculated based on these two pieces of information. For example, the "Arrival time" for the second customer is the arrival time of the previous customer plus the time between the first and the second customer (18.6+12.7-31.4). When this second customer arrives, the server is idle (since the first customer left at time 19.0) and, consequently, his service begins immediately (at his arrival time = 31.3); if the server had not been idle, he would have to wait for the previous customer to leave the system. The second customer ends his service (and leaves the system) at time 40.9 since he started his service at time 31.3 and his service took 9.6 time units. Thus, she spent 40.9-31.3 = 9.6 time units in the system. n 1 2 3 4 5 6 7 8 9 10 U 11 12 13 14 15 16 17 18 19 20 Interarrival times 18.6 12.7 36.0 22.7 36.1 25.7 31.9 39.9 26.7 15.8 11.6 44.1 16.6 16.9 38.8 34.7 11.5 36.4 12.6 11.6 Arrival time 18.6 31.3 67.3 Time service Service times begins 18.6 31.3 67.3 0.4 9.6 29.0 29.6 29.7 31.2 29.1 36.2 33.6 21.5 14.0 28.1 30.6 17.0 28.1 37.0 23.4 24.2 24.8 12.4 a) Complete the above table. b) Construct a graph of the number of customers in the system, N(t), vs. time, for 0 t 560. This graph should be like the one used in class to deduce Little's Law. Time service Time in the system 0.4 9.6 (t): No. of customers in the system ends 19.0 40.9 96.3 125.9 29.0 35.9 Waiting time 0.0 0.0 0.0 6.3 No. of customers in the system 0 30 60 90 120 150 180 210 240 270 300 330 360 390 420 450 480 510 540 Time (in minutes) c) Based on the information provided in the table and the graph that you constructed in (b), estimate: No. of arrivals 20 560 i. The average arrival rate = = -t T 1 ii. The average service rate = average service time iii. A 95% confidence for the mean service time (x-) = 0.03571 cust/min 1 24.48 tn-1=[20.16,28.80] n iv. A 95% confidence interval for the arrival rate. Using interarrival times data, the sample standard deviation, S, of the interarrival times is 11.26, the mean inter-arrival time is 560/20 = 28; and a 95% CI for the mean interarrival time; 1) Suppose there is a service center consisting of a single server. Let the external arrival process be Poisson with rate , and the service times be exponential with mean service-time 1/. The interarrival times (time between arrivals) and the service times of 20 customers have been recorded and they are shown in the table below; the other columns in the table can be calculated based on these two pieces of information. For example, the "Arrival time" for the second customer is the arrival time of the previous customer plus the time between the first and the second customer (18.6+12.7-31.4). When this second customer arrives, the server is idle (since the first customer left at time 19.0) and, consequently, his service begins immediately (at his arrival time = 31.3); if the server had not been idle, he would have to wait for the previous customer to leave the system. The second customer ends his service (and leaves the system) at time 40.9 since he started his service at time 31.3 and his service took 9.6 time units. Thus, she spent 40.9-31.3 = 9.6 time units in the system. n 1 2 3 4 5 6 7 8 9 10 U 11 12 13 14 15 16 17 18 19 20 Interarrival times 18.6 12.7 36.0 22.7 36.1 25.7 31.9 39.9 26.7 15.8 11.6 44.1 16.6 16.9 38.8 34.7 11.5 36.4 12.6 11.6 Arrival time 18.6 31.3 67.3 Time service Service times begins 18.6 31.3 67.3 0.4 9.6 29.0 29.6 29.7 31.2 29.1 36.2 33.6 21.5 14.0 28.1 30.6 17.0 28.1 37.0 23.4 24.2 24.8 12.4 a) Complete the above table. b) Construct a graph of the number of customers in the system, N(t), vs. time, for 0 t 560. This graph should be like the one used in class to deduce Little's Law. Time service Time in the system 0.4 9.6 (t): No. of customers in the system ends 19.0 40.9 96.3 125.9 29.0 35.9 Waiting time 0.0 0.0 0.0 6.3 No. of customers in the system 0 30 60 90 120 150 180 210 240 270 300 330 360 390 420 450 480 510 540 Time (in minutes) c) Based on the information provided in the table and the graph that you constructed in (b), estimate: No. of arrivals 20 560 i. The average arrival rate = = -t T 1 ii. The average service rate = average service time iii. A 95% confidence for the mean service time (x-) = 0.03571 cust/min 1 24.48 tn-1=[20.16,28.80] n iv. A 95% confidence interval for the arrival rate. Using interarrival times data, the sample standard deviation, S, of the interarrival times is 11.26, the mean inter-arrival time is 560/20 = 28; and a 95% CI for the mean interarrival time;