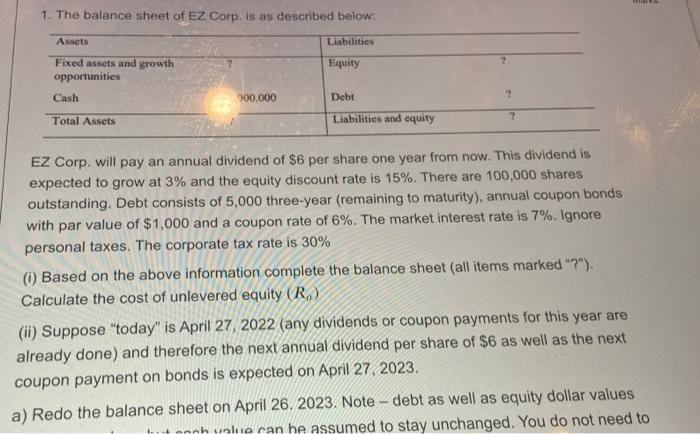
1. The balance sheet of EZ Corp. is as described below: Assets Liabilities Equity Fixed assets and growth opportunities Cash 900.000 Debt 2 Total Assets Liabilities and equity EZ Corp. will pay an annual dividend of $6 per share one year from now. This dividend is expected to grow at 3% and the equity discount rate is 15%. There are 100,000 shares outstanding. Debt consists of 5,000 three-year (remaining to maturity), annual coupon bonds with par value of $1,000 and a coupon rate of 6%. The market interest rate is 7%. Ignore personal taxes. The corporate tax rate is 30% (1) Based on the above information complete the balance sheet (all items marked "?"). Calculate the cost of unlevered equity (R) (ii) Suppose "today" is April 27, 2022 (any dividends or coupon payments for this year are already done) and therefore the next annual dividend per share of $6 as well as the next coupon payment on bonds is expected on April 27 2023, a) Redo the balance sheet on April 26. 2023. Note - debt as well as equity dollar values utannhvale can be assumed to stay unchanged. You do not need to (1) Based on the above information complete the balance sheo 1:57:59) Calculate the cost of unlevered equity (R) (i) Suppose "today is April 27, 2022 (any dividends or coupon payments for this year are already done) and therefore the next annual dividend per share of $6 as well as the next coupon payment on bonds is expected on April 27, 2023. a) Redo the balance sheet on April 26, 2023. Note - debt as well as equity dollar values should be redone but cash value can be assumed to stay unchanged. You do not need to redo any rates (le cost of my or debt) for this step and can assume these relevant rates are approximately unchang ake the usual assumption that dividend and coupon payments are instantaneous and costless. b) Based on the numbers calculated in il-a above, and assuming that cost of debt remains unchanged, calculate the new cost of equity (Rs). Note - now we are allowing cost of equity to change but are approximating such that we use the approximate dollar values calculated in il-a to get the numbers here. c) Based on these calculations what can you conclude about the manner in which cost of equity changes from the ex-dividend day after the payment of one dividend to the day before the next ex-dividend day (just under a year apart in this example)? Why? Keep your response to part c to 50 words or less. 1. The balance sheet of EZ Corp. is as described below: Assets Liabilities Equity Fixed assets and growth opportunities Cash 900.000 Debt 2 Total Assets Liabilities and equity EZ Corp. will pay an annual dividend of $6 per share one year from now. This dividend is expected to grow at 3% and the equity discount rate is 15%. There are 100,000 shares outstanding. Debt consists of 5,000 three-year (remaining to maturity), annual coupon bonds with par value of $1,000 and a coupon rate of 6%. The market interest rate is 7%. Ignore personal taxes. The corporate tax rate is 30% (1) Based on the above information complete the balance sheet (all items marked "?"). Calculate the cost of unlevered equity (R) (ii) Suppose "today" is April 27, 2022 (any dividends or coupon payments for this year are already done) and therefore the next annual dividend per share of $6 as well as the next coupon payment on bonds is expected on April 27 2023, a) Redo the balance sheet on April 26. 2023. Note - debt as well as equity dollar values utannhvale can be assumed to stay unchanged. You do not need to (1) Based on the above information complete the balance sheo 1:57:59) Calculate the cost of unlevered equity (R) (i) Suppose "today is April 27, 2022 (any dividends or coupon payments for this year are already done) and therefore the next annual dividend per share of $6 as well as the next coupon payment on bonds is expected on April 27, 2023. a) Redo the balance sheet on April 26, 2023. Note - debt as well as equity dollar values should be redone but cash value can be assumed to stay unchanged. You do not need to redo any rates (le cost of my or debt) for this step and can assume these relevant rates are approximately unchang ake the usual assumption that dividend and coupon payments are instantaneous and costless. b) Based on the numbers calculated in il-a above, and assuming that cost of debt remains unchanged, calculate the new cost of equity (Rs). Note - now we are allowing cost of equity to change but are approximating such that we use the approximate dollar values calculated in il-a to get the numbers here. c) Based on these calculations what can you conclude about the manner in which cost of equity changes from the ex-dividend day after the payment of one dividend to the day before the next ex-dividend day (just under a year apart in this example)? Why? Keep your response to part c to 50 words or less