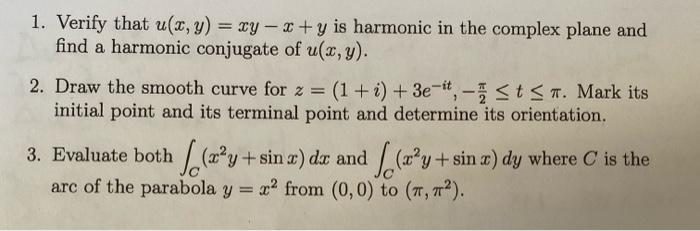
1. Verify that u(x, y) = xy-x+y is harmonic in the complex plane and find a harmonic conjugate of u(x, y). 2. Draw the smooth curve for z = (1+i) + 3eit, -t T. Mark its initial point and its terminal point and determine its orientation. 3. Evaluate both (xy + sin x) dr and f(xy + sin x) dy where C is the arc of the parabola y = x from (0,0) to (, 2).