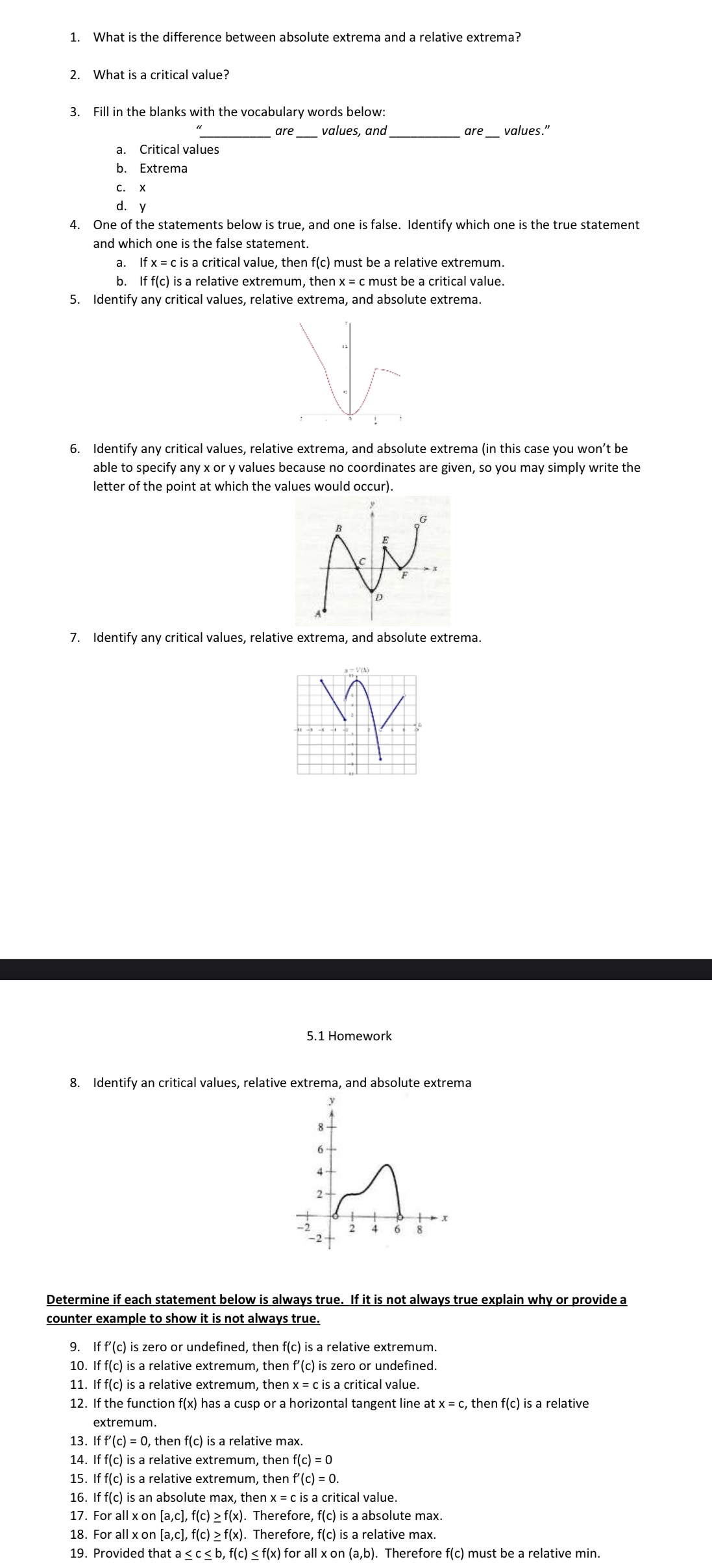
1. What is the difference between absolute extrema and a relative extrema? 2. What is a critical value? 3. Fill in the blanks with the vocabulary words below: 11 are values, and a. b. Critical values Extrema C. X d. y 4. One of the statements below is true, and one is false. Identify which one is the true statement and which one is the false statement. a. If x= c is a critical value, then f(c) must be a relative extremum. b. If f(c) is a relative extremum, then x = c must be a critical value. 5. Identify any critical values, relative extrema, and absolute extrema. 6. Identify any critical values, relative extrema, and absolute extrema (in this case you won't be able to specify any x or y values because no coordinates are given, so you may simply write the letter of the point at which the values would occur). AN a = V(A) W 7. Identify any critical values, relative extrema, and absolute extrema. 5.1 Homework 8 are 8. Identify an critical values, relative extrema, and absolute extrema 6 G y A 2 4 6 values." 8 Determine if each statement below is always true. If it is not always true explain why or provide a counter example to show it is not always true. 9. If f'(c) is zero or undefined, then f(c) is a relative extremum. 10. If f(c) is a relative extremum, then f'(c) is zero or undefined. 11. If f(c) is a relative extremum, then x = c is a critical value. 12. If the function f(x) has a cusp or a horizontal tangent line at x = c, then f(c) is a relative extremum. 13. If f'(c) = 0, then f(c) is a relative max. 14. If f(c) is a relative extremum, then f(c) = 0 15. If f(c) is a relative extremum, then f'(c) = 0. 16. If f(c) is an absolute max, then x = c is a critical value. 17. For all x on [a,c], f(c) > f(x). Therefore, f(c) is a absolute max. 18. For all x on [a,c], f(c) f(x). Therefore, f(c) is a relative max. 19. Provided that a c b, f(c) < f(x) for all x on (a,b). Therefore f(c) must be a relative min.