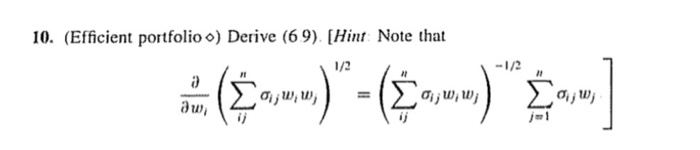
10. (Efficient portfolioo) Derive (6 9) Hint Note that 1/2 uw iju),w How can we find the tangent point that represents the efficient fund? We just character- ize that point in terms of an optimization problem Given a point in the feasible region. we draw a line between the risk-free asset and that point We denote the angle between that line and the horizontal axis by 8 For any feasible (risky) portfolio p, we have The tangent portfolio is the feasible point that maximizes or, equivalently, maxi- mizes tan It turns out that this problem can be reduced to the solution of a system of linear equations To develop the solution, suppose, as usual, that there are isky assets We assign weights w. . ww to the tisky assets such that L 1 There is zero weight on the risk-free asset in the tangent fund (Note that we are allowing short selling among the risky assets ) For ,,-E: us ,. we have F.-,wi, and Thus, tan = pter 6 MEAN-VARIANCE PORTFOLIO THEORY It should be clear that multiplication of all w's by a constant will not change the expression, since the constant will cancel Hence t is not necessary to impose the constraint .1 u-l here We then set the derivative of tane with respect to each w equal to zero This leads (see Exercise 10) to the following equations: (69) where is an (unknown) constant Making the substitution becomes w; for each i. (69) (6.10) We solve these linear equations for the v's and then normalize to determine the w's that is Vi 10. (Efficient portfolioo) Derive (6 9) Hint Note that 1/2 uw iju),w How can we find the tangent point that represents the efficient fund? We just character- ize that point in terms of an optimization problem Given a point in the feasible region. we draw a line between the risk-free asset and that point We denote the angle between that line and the horizontal axis by 8 For any feasible (risky) portfolio p, we have The tangent portfolio is the feasible point that maximizes or, equivalently, maxi- mizes tan It turns out that this problem can be reduced to the solution of a system of linear equations To develop the solution, suppose, as usual, that there are isky assets We assign weights w. . ww to the tisky assets such that L 1 There is zero weight on the risk-free asset in the tangent fund (Note that we are allowing short selling among the risky assets ) For ,,-E: us ,. we have F.-,wi, and Thus, tan = pter 6 MEAN-VARIANCE PORTFOLIO THEORY It should be clear that multiplication of all w's by a constant will not change the expression, since the constant will cancel Hence t is not necessary to impose the constraint .1 u-l here We then set the derivative of tane with respect to each w equal to zero This leads (see Exercise 10) to the following equations: (69) where is an (unknown) constant Making the substitution becomes w; for each i. (69) (6.10) We solve these linear equations for the v's and then normalize to determine the w's that is Vi