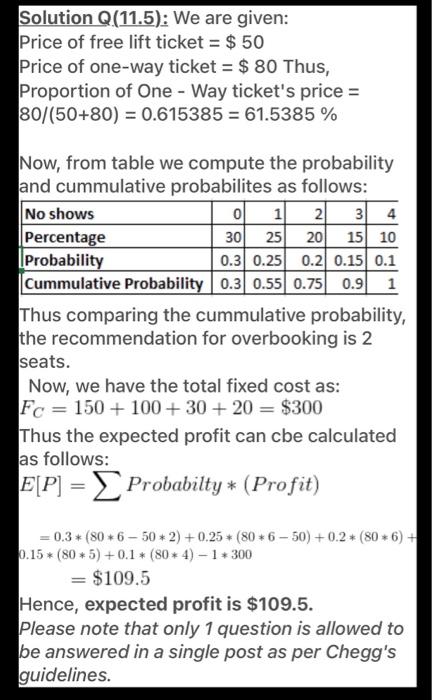
11.8. Reconsider Example 11.5 (Blackjack Airline). After initial success with the Los Angeles-to-Las Vegas route, Blackjack Airline's demand for full-fare tickets has increased to an average of 75, with the standard deviation remaining at 15. Consequently, Blackjack has decided to raise all ticket prices by $10. Under these new conditions, how many full-fare seats should Blackjack reserve? Solution Q.(11.5): We are given: Price of free lift ticket = $50 Price of one-way ticket = $ 80 Thus, Proportion of One - Way ticket's price = 80/(50+80) = 0.615385 = 61.5385 % 0 Now, from table we compute the probability and cummulative probabilites as follows: No shows 1 2 314 Percentage 30 25 20 15| 10 Probability 0.3 0.25 0.21 0.15 0.1 Cummulative Probability 0.3 0.55 0.75 0.91 Thus comparing the cummulative probability, the recommendation for overbooking is 2 seats. Now, we have the total fixed cost as: Fc = 150 + 100+ 30 + 20 = $300 Thus the expected profit can cbe calculated as follows: E[P] = Probabilty* (Profit) = 0.3+ (80 * 6 - 50 + 2) +0.25 + (80 * 6 - 50) +0.2 + (80 + 6) + 0.15 * (80 * 5) + 0.1 * (80+ 4) 1* 300 = $109.5 Hence, expected profit is $109.5. Please note that only 1 question is allowed to be answered in a single post as per Chegg's guidelines. 11.8. Reconsider Example 11.5 (Blackjack Airline). After initial success with the Los Angeles-to-Las Vegas route, Blackjack Airline's demand for full-fare tickets has increased to an average of 75, with the standard deviation remaining at 15. Consequently, Blackjack has decided to raise all ticket prices by $10. Under these new conditions, how many full-fare seats should Blackjack reserve? Solution Q.(11.5): We are given: Price of free lift ticket = $50 Price of one-way ticket = $ 80 Thus, Proportion of One - Way ticket's price = 80/(50+80) = 0.615385 = 61.5385 % 0 Now, from table we compute the probability and cummulative probabilites as follows: No shows 1 2 314 Percentage 30 25 20 15| 10 Probability 0.3 0.25 0.21 0.15 0.1 Cummulative Probability 0.3 0.55 0.75 0.91 Thus comparing the cummulative probability, the recommendation for overbooking is 2 seats. Now, we have the total fixed cost as: Fc = 150 + 100+ 30 + 20 = $300 Thus the expected profit can cbe calculated as follows: E[P] = Probabilty* (Profit) = 0.3+ (80 * 6 - 50 + 2) +0.25 + (80 * 6 - 50) +0.2 + (80 + 6) + 0.15 * (80 * 5) + 0.1 * (80+ 4) 1* 300 = $109.5 Hence, expected profit is $109.5. Please note that only 1 question is allowed to be answered in a single post as per Chegg's guidelines