13. (3 points) Consider a scalar-valued random variable X that takes values {1,2,3,4} with probabilities Px(1) = 0.2, px (2) = 0.3, px(3) = 0.25, and px (4) = 0.25. Compute the mean and variance of X. 14. (2 points) Consider a random vector X ERP and let E[X] :=u. Define another random vector Y as Y = X-u. What is E[Y]? Justify your answer using your knowledge of (i) linearity of the expectation of a random variable and (ii) definition of the mean of a random vector. 15. Consider a random vector X = X1 X2 X3' such that the pairs of random variables (X1, X2), (X1, X3), and (X2, X3) are statistically independent. Further, let X be distributed as Gaussian(-1,2), X2 be distributed as Bernoulli(0.5) and, X3 be distributed as continuous-valued) uniform(3,6). 1. (2 points) Compute the mean vector i=EX. 2. (3 points) Compute the covariance matrix C = E(X- X-H)]. Hint: It is worth remem- bering that if two random variables U and V are statistically independent then Eh(U)g(V) = E[h(U)]E[9(V)] for any functions h) and g). 16. (5 points) Consider a random variable Y that is defined as Y = a +W, where a is a constant and W is a random variable with mean 0 and variance 1. Suppose we are given n independent realizations of Y, given by Yi, i = 1,...,n. Show that a = - Y; has mean a and variance that satisfies limto var(a) = 0. Note: This is an example of the Law of Large Numbers (LLN), which essentially says that averaging a large number of independent random variables gives us an almost deterministic quantity.

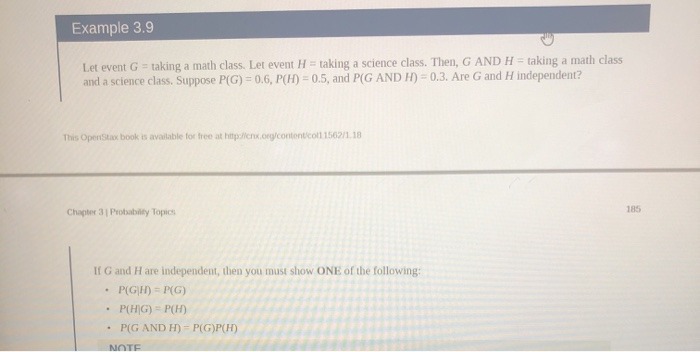
13. (3 points) Consider a scalar-valued random variable X that takes values {1, 2,3, 4} with probabilities px (1) = 0.2, px (2) = 0.3, px (3) = 0.25, and px(4) = 0.25. Compute the mean and variance of X. 14. (2 points) Consider a random vector X e RP and let E[X] := p. Define another random vector Y as Y = X- u. What is E Y)? Justify your answer using your knowledge of () linearity of the expectation of a random variable and (di) definition of the mean of a random vector. 15. Consider a random vector X = X1 X2 Xs such that the pairs of random variables (X1, X2), (X1, Xs), and (X2, X3) are statistically independent. Further, let X1 be distributed as Gaussian(-1, 2), X2 be distributed as Bernoulli(0.5) and, X's be distributed as (continuous-valued) uniform [3, 6]. 1. (2 points) Compute the mean vector / = E X]. 2. (3 points) Compute the covariance matrix C = E[(X - )(X - p) ]. Hint: It is worth remem- bering that if two random variables / and V are statistically independent then Efh(U)g (V)] = Ejh(U)]E[g(V)] for any functions h(.) and g(.). 16. (5 points) Consider a random variable Y that is defined as Y = a + W, where a is a constant and W is a random variable with mean 0 and variance 1. Suppose we are given n independent realizations of Y, given by Y,,i = 1. ...,n. Show that a = _ _ _ Y, has mean a and variance that satisfies lim,-+ var(a) =0. Note: This is an example of the Law of Large Numbers (LLN), which essentially says that averaging a large number of independent random variables gives us an almost deterministic quantity.Example 3.9 Let event G = taking a math class. Let event H = taking a science class. Then, G AND H = taking a math class and a science class. Suppose P(G) = 0.6, P(H) = 0.5, and P(G AND H) = 0.3. Are G and H independent? This OpenStax book is available for free at hipaliens. org/contentcol1 1562/1,18 Chapter 3 | Probability Topics 185 If G and H are independent, then you must show ONE of the following: . P(GH) = P(G) . P(HG) = P(H) . P(G AND H) =P(G)P(H)