






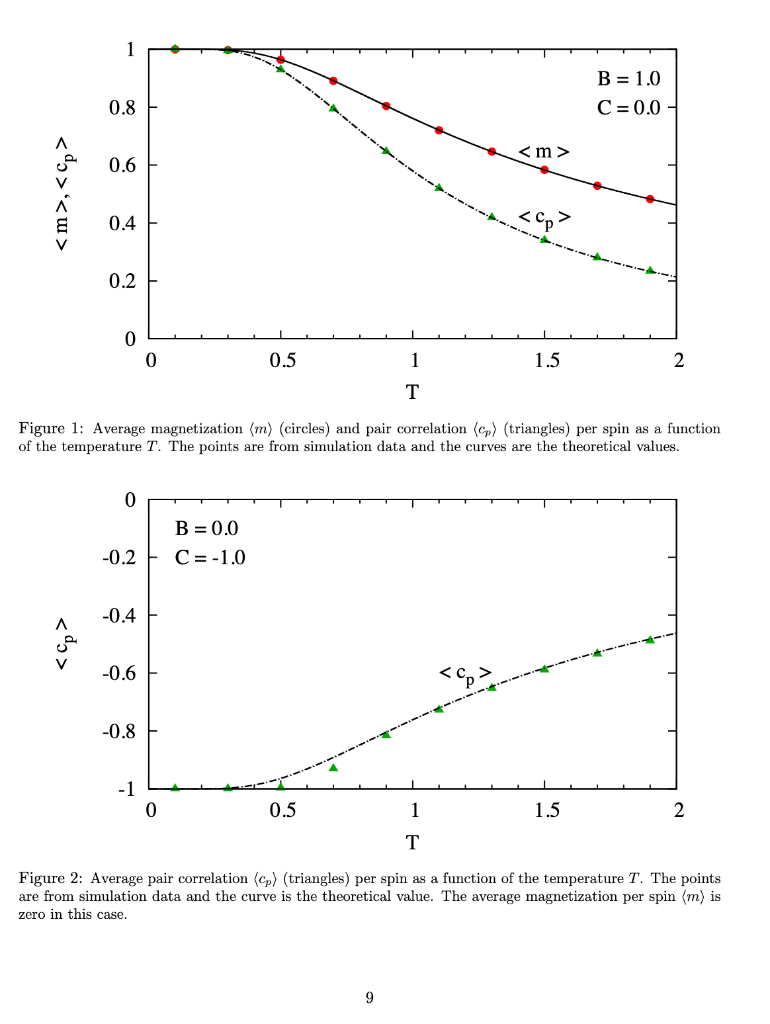




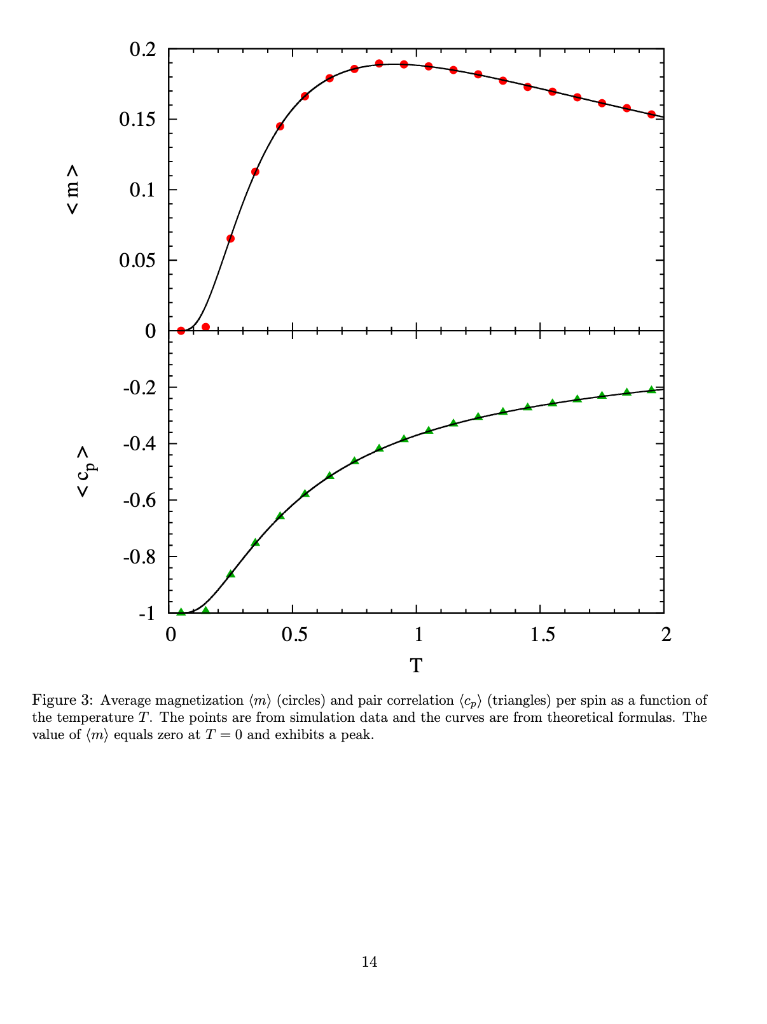
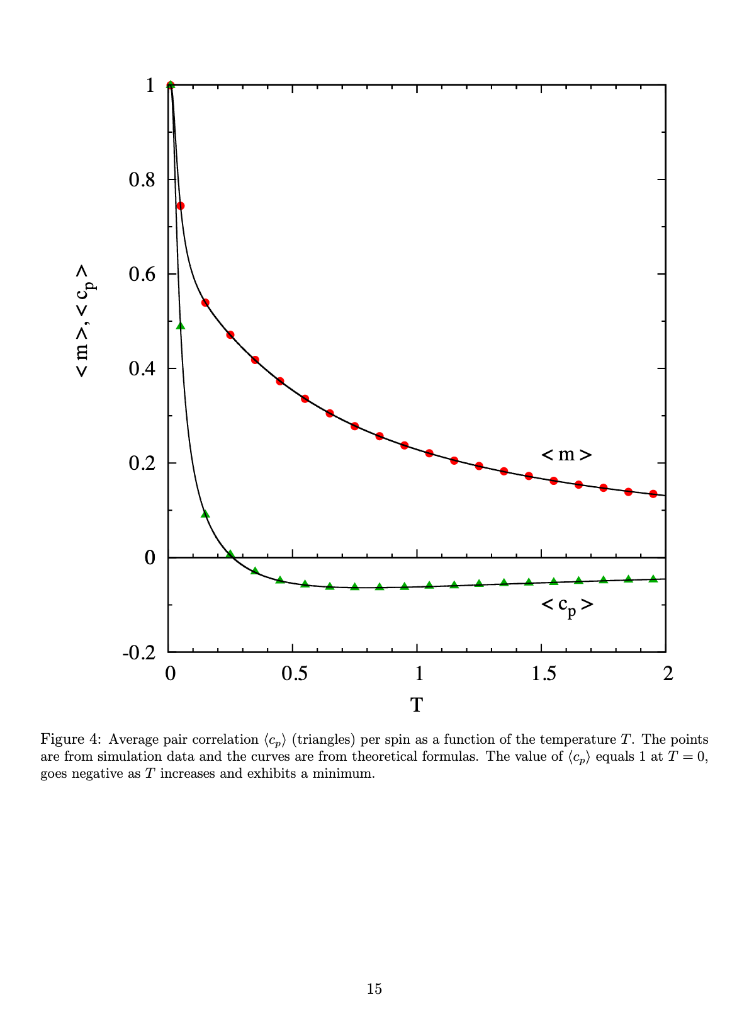
1.3 Some quantum physics don't panic These are definitions, nothing to compute here. o We shall calculate some thermodynamic properties of a set of quantum spins 1. A quantum spin s, is a variable which can take only two values s 2. There are n quantum spins si, i -1,...,n 3. The spins are arranged in a circle, so each spin has two neighbors (circular linked list) 4. For 1 0 then compute p-e-,1)/T, Note that 0 0, point all the spins up s 1 2. If C 0, the spins like to be parallel . . . or because then 8i8i+1 = 1 and C'siS+1 > 0 2. If C0 3. The case C 0 is ambiguous but we can go with parallel spins Note also that there is no purpose in using B -B, just flip all the spins si --si and we obtain the same result 2. This is because Bs-(-B)(-si) and the product of spins is not affected if we flip all the spins: sisi +1=(-six-si+1) 3. Hence we shall use B > 0 in our calculations 4. Note that if B> 0 then the spins like up point up si-1 because then Bsi> 0 5. If B- 0, the term in C will determine the spin configuration Of course, if B > 0 and C 0 and C 0 then the spins want to be up si = 1 but if C 0 and C 0. The peak is unique. The graph of (m) does not have multiple peaks 2. The graph in Fig. 4 used different alues B > 0 and C 0 and C 0 2. Find values B > 0 and C 0 and C 0 and C 0 What is the highest peak value you can obtain for (m)? . Challenge #5: (Extension of Challenge #2.) Find values for B > 0 and C 0 What is the lowest minimum (most negative value) you can obtain for (cp)? 13 0.2 0.15 E 0.1 0.05 0 0.2 A -0.4 V 0.6 0.8 -1 0 0.5 1.5 2 Figure 3: Average magnetization (m) (circles) and pair correlation cs) (triangles) per spin as a function of the temperature T. The points are from simulation data and the curves are from theoretical formulas. The value of (m) equals zero at T-0 and exhibits a peak 14 0.8 0 A 0.6 0.4 0.2 0 0.2 0 0.5 1.5 2 Figure 4: Average pair correlation (cp) (triangles) per spin as a function of the temperature T. The points are from simulation data and the curves are from theoretical formulas. The value of (co) equals 1 at T = 0, goes negative as T increases and exhibits a minium 15 1.3 Some quantum physics don't panic These are definitions, nothing to compute here. o We shall calculate some thermodynamic properties of a set of quantum spins 1. A quantum spin s, is a variable which can take only two values s 2. There are n quantum spins si, i -1,...,n 3. The spins are arranged in a circle, so each spin has two neighbors (circular linked list) 4. For 1 0 then compute p-e-,1)/T, Note that 0 0, point all the spins up s 1 2. If C 0, the spins like to be parallel . . . or because then 8i8i+1 = 1 and C'siS+1 > 0 2. If C0 3. The case C 0 is ambiguous but we can go with parallel spins Note also that there is no purpose in using B -B, just flip all the spins si --si and we obtain the same result 2. This is because Bs-(-B)(-si) and the product of spins is not affected if we flip all the spins: sisi +1=(-six-si+1) 3. Hence we shall use B > 0 in our calculations 4. Note that if B> 0 then the spins like up point up si-1 because then Bsi> 0 5. If B- 0, the term in C will determine the spin configuration Of course, if B > 0 and C 0 and C 0 then the spins want to be up si = 1 but if C 0 and C 0. The peak is unique. The graph of (m) does not have multiple peaks 2. The graph in Fig. 4 used different alues B > 0 and C 0 and C 0 2. Find values B > 0 and C 0 and C 0 and C 0 What is the highest peak value you can obtain for (m)? . Challenge #5: (Extension of Challenge #2.) Find values for B > 0 and C 0 What is the lowest minimum (most negative value) you can obtain for (cp)? 13 0.2 0.15 E 0.1 0.05 0 0.2 A -0.4 V 0.6 0.8 -1 0 0.5 1.5 2 Figure 3: Average magnetization (m) (circles) and pair correlation cs) (triangles) per spin as a function of the temperature T. The points are from simulation data and the curves are from theoretical formulas. The value of (m) equals zero at T-0 and exhibits a peak 14 0.8 0 A 0.6 0.4 0.2 0 0.2 0 0.5 1.5 2 Figure 4: Average pair correlation (cp) (triangles) per spin as a function of the temperature T. The points are from simulation data and the curves are from theoretical formulas. The value of (co) equals 1 at T = 0, goes negative as T increases and exhibits a minium 15




















