Question: 13. The observed mean is less than 2.575 standard errors above the hypothesized mean [Quality Control Process]. A. True B. False 14. If the null

![the hypothesized mean [Quality Control Process]. A. True B. False 14. If](https://s3.amazonaws.com/si.experts.images/answers/2024/06/66699027cb37e_21566699027b9c4d.jpg)
![size 36) will be below 20 cm. [Quality Control Process]. A. True](https://s3.amazonaws.com/si.experts.images/answers/2024/06/666990289df38_216666990285f36d.jpg)
![at the alpha=.05 level of significance [Charlie's Productivity]. A. True B. False](https://s3.amazonaws.com/si.experts.images/answers/2024/06/666990293f3b9_217666990292d8e0.jpg)

![would produce an observed t- value of +2.0 [Charlie's Productivity]- A. True](https://s3.amazonaws.com/si.experts.images/answers/2024/06/66699029dd7bb_21766699029cb79a.jpg)
![t-distribution with $ degrees of freedom [Charlie's Productivity]. A. True B. False](https://s3.amazonaws.com/si.experts.images/answers/2024/06/6669902a779fe_2186669902a5b669.jpg)
![testing at either alpha=.05 or alpha=.01 [Charlie's Productivity]- A. True B. False](https://s3.amazonaws.com/si.experts.images/answers/2024/06/6669902b1474b_2186669902aef196.jpg)

![the sample is less than 30 boxes [ Cereal Package Filling] A.](https://s3.amazonaws.com/si.experts.images/answers/2024/06/6669902bd052d_2196669902b9c53c.jpg)
![oz. [Cereal Package Filling]- A. True B. False 21. We can conclude,](https://s3.amazonaws.com/si.experts.images/answers/2024/06/6669902c81ed0_2206669902c60470.jpg)
![at a=0.05, that the machine is overfilling [Cereal Package Filling].. A. True](https://s3.amazonaws.com/si.experts.images/answers/2024/06/6669902ccc245_2206669902cb87ae.jpg)
![.05. [Mean valuation of homes] A. True B. False 23. Using a](https://s3.amazonaws.com/si.experts.images/answers/2024/06/6669902dcf6b7_2216669902dbf528.jpg)

![than +1.96. [Mean valuation of homes] A. True B. False 24. Since](https://s3.amazonaws.com/si.experts.images/answers/2024/06/6669902ed63a1_2226669902eb7760.jpg)
![error is only .05 (or 5%) [Chewie-Chocolate Candies]. A. True B. False[Hypothesis](https://s3.amazonaws.com/si.experts.images/answers/2024/06/6669902f8480a_2236669902f60e45.jpg)
![Testing - Proportions] A pharmaceutical firm, BigPharm, claims to have developed a](https://s3.amazonaws.com/si.experts.images/answers/2024/06/6669902feb26c_2236669902fd97d2.jpg)


![the trial subjects [p=384/600=64%]. Is BigPharm's claim (the research hypothesis) supported at](https://s3.amazonaws.com/si.experts.images/answers/2024/06/6669903180a96_225666990315dd88.jpg)


![SJNV(D.95,1)=+1.645 Criterion for decision: Reject Ho if [Zo 2 +1.645], failed to](https://s3.amazonaws.com/si.experts.images/answers/2024/06/6669903372e18_227666990333a96a.jpg)
![reject otherwise. OR = V[(P) (1-P)] = [(.60*.40)/600] = 2% Zo =](https://s3.amazonaws.com/si.experts.images/answers/2024/06/66699033bfee5_22766699033aacf0.jpg)
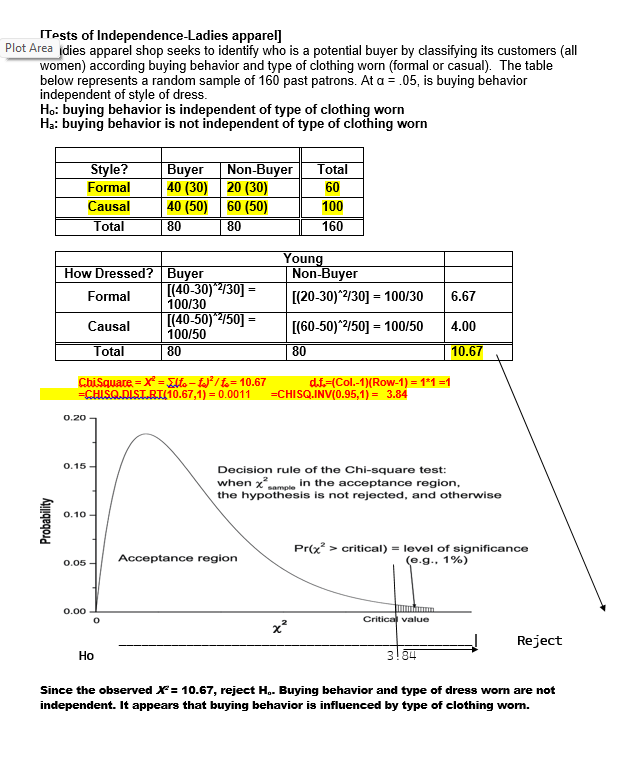
![drug should be approved.[Tests of Independence-Ladies apparel] Plot Area idies apparel shop](https://s3.amazonaws.com/si.experts.images/answers/2024/06/66699034ba061_22866699034a3376.jpg)
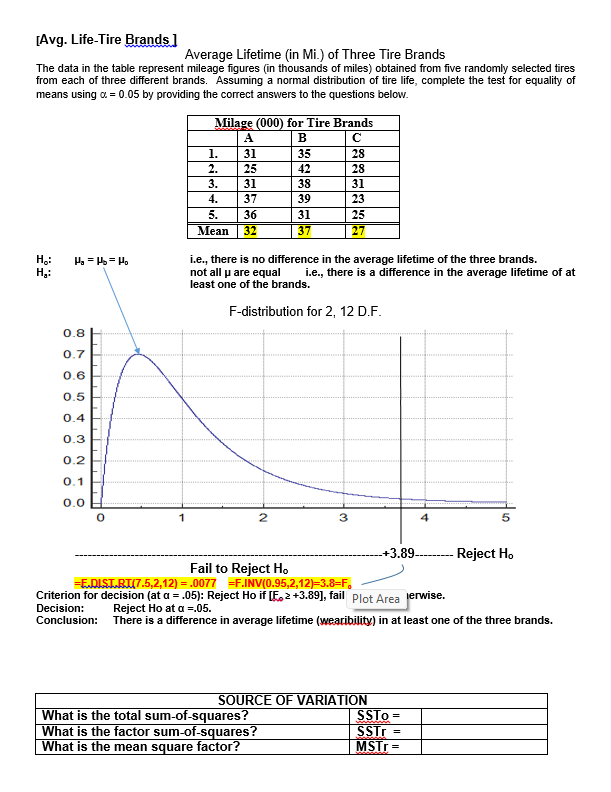
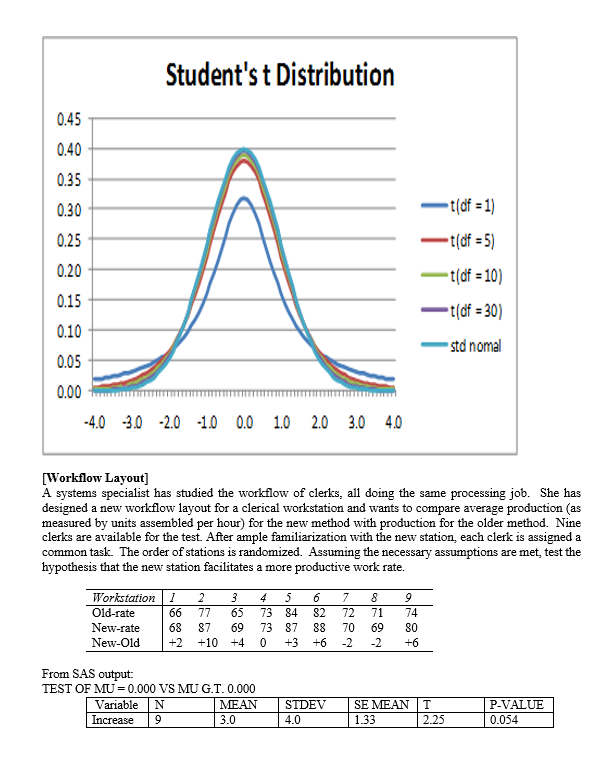
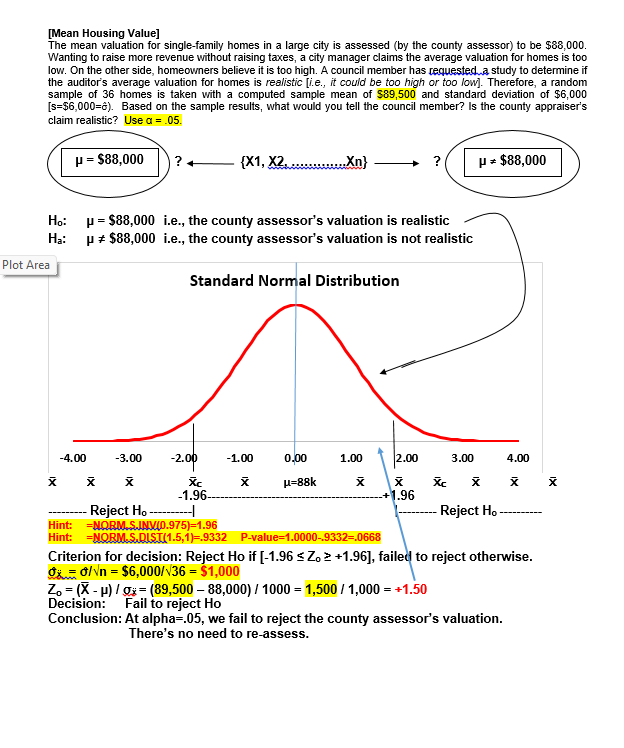
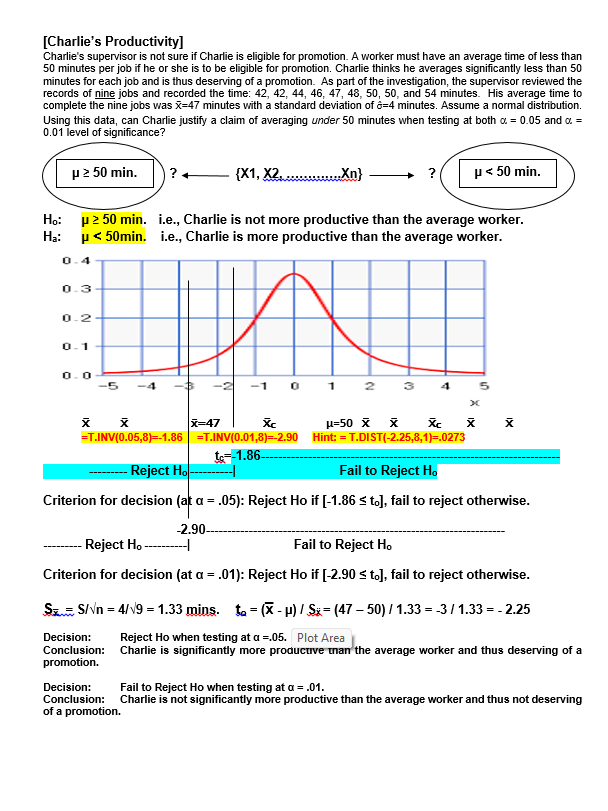
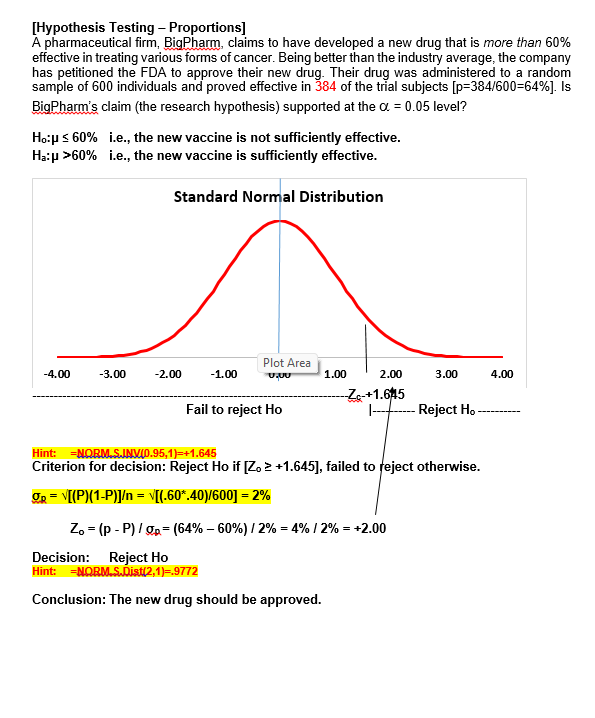
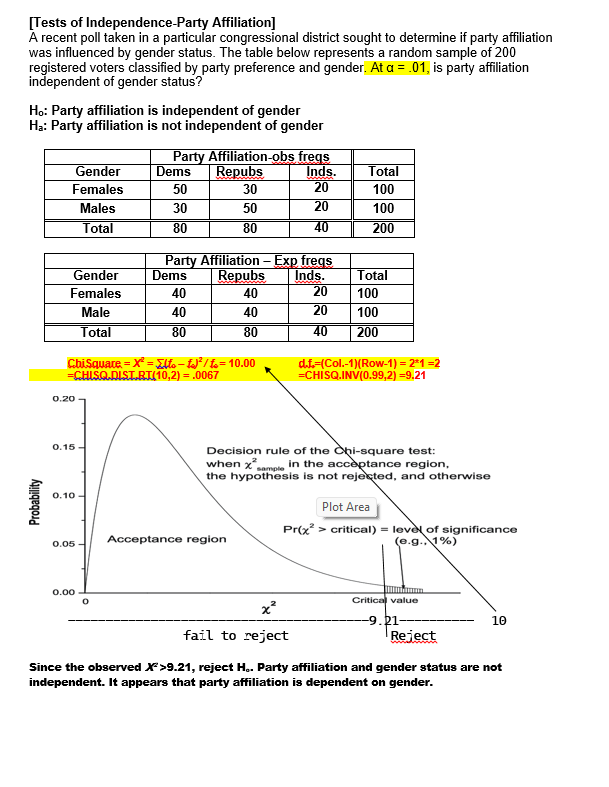
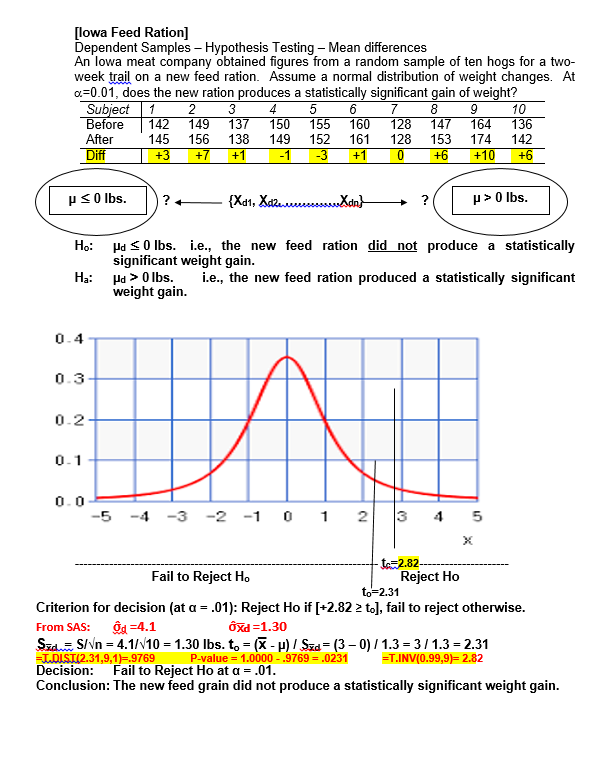
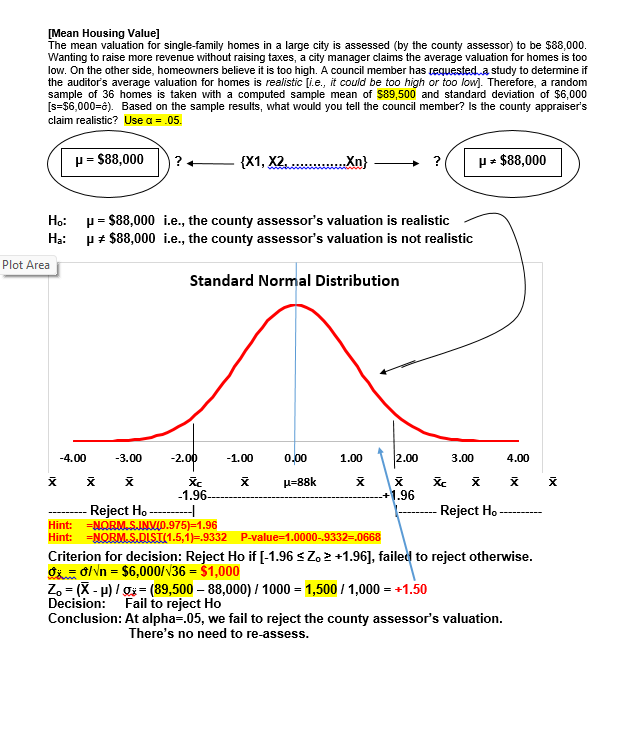
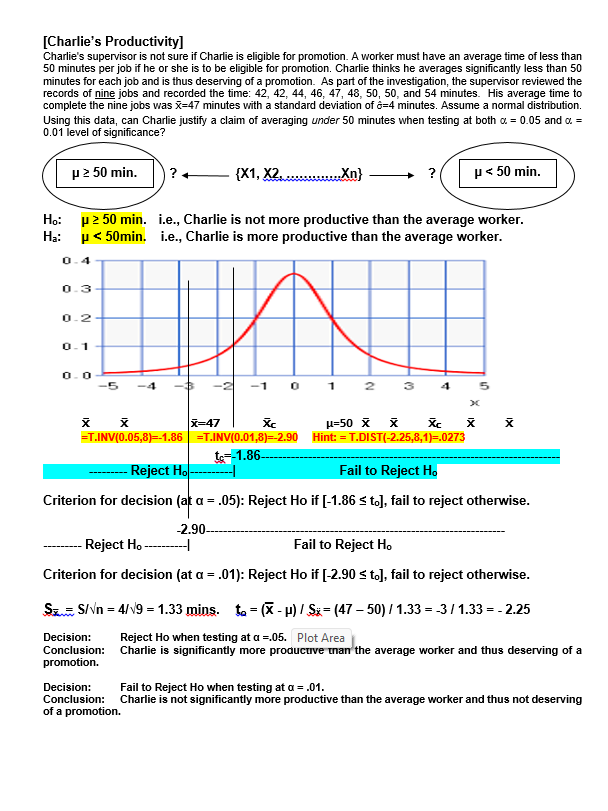
13. The observed mean is less than 2.575 standard errors above the hypothesized mean [Quality Control Process]. A. True B. False 14. If the null hypothesis is correct, then 99.87% of all sample means (of size 36) will be below 20 cm. [Quality Control Process]. A. True B. False 15. We reject the null hypothesis at alpha=.01 but not at the alpha=.05 level of significance [Charlie's Productivity]. A. True B. False 16. An observed sample mean that is 2.66 minutes below 50.0 minutes would produce an observed t- value of +2.0 [Charlie's Productivity]- A. True B. False 17. For this problem, the appropriate test statistic is a t-distribution with $ degrees of freedom [Charlie's Productivity]. A. True B. False 18. Based on sample results, we would reject the null hypothesis when testing at either alpha=.05 or alpha=.01 [Charlie's Productivity]- A. True B. False 19. For this problem, the null hypothesis can not be tested because the sample is less than 30 boxes [ Cereal Package Filling] A. True B. False 20. The standard error of the mean is 0.01 oz. [Cereal Package Filling]- A. True B. False 21. We can conclude, at a=0.05, that the machine is overfilling [Cereal Package Filling].. A. True B. False 22. The difference between the estimated and hypothesized mean would have to be at least $6,000 to be significant at a = .05. [Mean valuation of homes] A. True B. False 23. Using a = .05, the appropriate criterion for decision is to reject Ho if the calculated (or sample) "z" statistic is less than -1.96 or greater than +1.96. [Mean valuation of homes] A. True B. False 24. Since this is a one-tailed test, the probability of committing a Type I error is only .05 (or 5%) [Chewie-Chocolate Candies]. A. True B. False[Hypothesis Testing - Proportions] A pharmaceutical firm, BigPharm, claims to have developed a new drug that is more than 60% effective in treating various forms of cancer. Being better than the industry average, the company has petitioned the FDA to approve their new drug. Their drug was administered to a random sample of 600 individuals and proved effective in 384 of the trial subjects [p=384/600=64%]. Is BigPharm's claim (the research hypothesis) supported at the of = 0.05 level? Hop $ 60% i.e., the new vaccine is not sufficiently effective. Ha:[ >60% i.e., the new vaccine is sufficiently effective. Standard Normal Distribution Plot Area -4.00 -3.00 -2.00 -1.00 U.UU 1.00 2.00 3.00 4.00 Zc-+1.645 Fail to reject Ho Reject Ho Hint: =NORM. SJNV(D.95,1)=+1.645 Criterion for decision: Reject Ho if [Zo 2 +1.645], failed to reject otherwise. OR = V[(P) (1-P)] = [(.60*.40)/600] = 2% Zo = (p - P) / ga= (64% - 60%) / 2% = 4% / 2% = +2.00 Decision: Reject Ho Hint: =NORM.S.Dist(2,1)=.9772 Conclusion: The new drug should be approved.[Tests of Independence-Ladies apparel] Plot Area idies apparel shop seeks to identify who is a potential buyer by classifying its customers (all women) according buying behavior and type of clothing worn (formal or casual). The table below represents a random sample of 160 past patrons. At a = .05, is buying behavior independent of style of dress. Ho: buying behavior is independent of type of clothing worn Ha: buying behavior is not independent of type of clothing worn Style? Buyer Non-Buyer Total Forma 40 (30 20 (30) 60 Causal 40 (50) 60 (50) 100 Total 80 80 160 Young How Dressed? Buyer Non-Buyer Formal [(40-30) '430] = 100/30 [(20-30)*230] = 100/30 6.67 Causal [(40-50) 450] = 100/50 [(60-50)*250] = 100/50 4.00 Total 80 80 10.67 ChiSquare = X' = Elto -f / to= 10.67 d.f.=(Col.-1)(Row-1) = 131 =1 -CHISQ.DIST.RT(10.67,1) = 0.0011 =CHISQ.INV(0.95,1) = 3.84 0.20 0.15 - Decision rule of the Chi-square test: when x"in the acceptance region, the hypothesis is not rejected, and otherwise 0.10 - Probability Pr(x> > critical) = level of significance 0.05 - Acceptance region (e.g., 1%) 0.00 0 Critical value Reject Ho 3!84 Since the observed X= 10.67, reject H.. Buying behavior and type of dress worn are not independent. It appears that buying behavior is influenced by type of clothing worn.[Tests of Independence-Party Affiliation] A recent poll taken in a particular congressional district sought to determine if party affiliation was influenced by gender status. The table below represents a random sample of 200 registered voters classified by party preference and gender. At a = 01, is party affiliation independent of gender status? Ho: Party affiliation is independent of gender Ha: Party affiliation is not independent of gender Party Affiliation-obs freqs Gender Dems Repubs Inds. Total Females 50 30 20 100 Males 30 50 20 100 Total 80 80 40 200 Party Affiliation - Exp freqs Gender Dems Repubs Inds. Total Females 10 10 20 100 Male 40 40 20 100 Total 80 80 40 200 ChiSquare = X =Elf. -fJ'/fo=10.00 d.f.=(Col.-1)(Row-1) = 2*1 =2 CHISQ.DIST.RT(10,2) = .0067 =CHISQ.INV(0.99,2) =9.21 0.20 0.15 Decision rule of the Chi-square test: when x" in the acceptance region, the hypothesis is not rejected, and otherwise 0.10 Probability Plot Area Pr(x7 > critical) = level of significance 0.05 - Acceptance region (e.g., 1%) 0.00 Critical value x -9. 21- 10 fail to reject Reject Since the observed X">9.21, reject H.. Party affiliation and gender status are not independent. It appears that party affiliation is dependent on gender.[Avg. Life-Tire Brands ] Average Lifetime (in Mi.) of Three Tire Brands The data in the table represent mileage figures (in thousands of miles) obtained from five randomly selected tires from each of three different brands. Assuming a normal distribution of tire life, complete the test for equality of means using F Treatment 168.00 84.00 25.20 0.0002 Error 30.00 3.33 Total 11 198.00 Comparisons significant at the 0.05 level are indicated by ***. Difference Simultaneous Gasbrand Between 95% Confidence Comparison Means Limits C 3.000 -0.767 -- 6.767 C 9.000 5.233 -- 12.767 a -3.000 -6.767 -- 0.767 6.000 2.233 -- 9.767 * * Plot AreaSchematic Dependent Sample Design Hypothesis Testing - One Mean For X-bar -Use MS Reference San Serif and character code "F7C2" Ho: Ud = 0 (X1, X2 X3 ....... XO ? (Xid, Xzd,Xeg ... Xnl? Ha: Jud = ### (X1, X2, X3 ....... XD Xd = EXi Oxd = 6d/ Vn 0 t-dis, df-n-1 Xd i = k Plot Area[lowa Feed Ration] Dependent Samples - Hypothesis Testing - Mean differences An lowa meat company obtained figures from a random sample of ten hogs for a two- week trail on a new feed ration. Assume a normal distribution of weight changes. At =0.01, does the new ration produces a statistically significant gain of weight? Subject 1 2 3 4 5 8 9 10 Before 142 149 137 150 155 160 128 147 164 136 After 145 156 138 149 152 161 128 153 174 142 Diff +3 +7 +1 -1 +1 0 +6 +10 +6 P 5 0 lbs. ? # P > 0 lbs. Ho: Ud 0 lbs. i.e., the new feed ration produced a statistically significant weight gain. 0.4 0.3 0.2- 0- 1 0. 0 -5 -4 -3 -2 -1 0 1 3 4 5 X to= 2.82 Fail to Reject Ho Reject Ho to=2.31 Criterion for decision (at a = .01): Reject Ho if [+2.82 > to], fail to reject otherwise. From SAS: Od =4.1 OXd =1.30 Sad.= S/Vn = 4.1/V10 = 1.30 lbs. to = (x - p) / Sza= (3 - 0) / 1.3 = 3/ 1.3 =2.31 T.DIST(2.31,9,1)=.9769 P-value = 1.0000 - .9769 = .0231 T.INV(0.99,9)= 2.82 Decision: Fail to Reject Ho at a = .01. Conclusion: The new feed grain did not produce a statistically significant weight gain.Student's t Distribution 0.45 0.40 0.35 0.30 -t( of = 1) 0.25 -t( of = 5) 0.20 -t(of = 10) 0.15 t( of = 30) 0.10 std nomal 0.05 0.00 4.0 -3.0 -2.0 -1.0 0.0 1.0 2.0 3.0 4.0 [Workflow Layout] A systems specialist has studied the workflow of clerks, all doing the same processing job. She has designed a new workflow layout for a clerical workstation and wants to compare average production (as measured by units assembled per hour) for the new method with production for the older method. Nine clerks are available for the test. After ample familiarization with the new station, each clerk is assigned a common task. The order of stations is randomized. Assuming the necessary assumptions are met, test the hypothesis that the new station facilitates a more productive work rate. Workstation ] 2 3 4 5 6 7 8 9 Old-rate 66 77 65 73 84 82 72 71 74 New-rate 68 87 69 73 87 88 70 69 80 New-Old +2 +10 +4 0 +3 +6 -2 -2 +6 From SAS output: TEST OF MU = 0.000 VS MU G.T. 0.000 Variable N MEAN STDEV SE MEAN T P-VALUE Increase 9 3.0 4.0 1.33 2.25 0.05425. The "p" value of the calculated (or observed) test statistic is .0228 [Chewie-Chocolate Candies]. A. True B. False 26. Based on the evidence presented, we can conclude (Using a = 0.10) that the average weight is less than 2.00 ounces [Chewie-Chocolate Candies]. A. True B. False 27. Charlie can justify a claim of averaging under 30 minutes when testing at a=0.05 level, but not at the a=0.01 level of significance [Charlie's Productivity]. A. True B. False 28. If the null hypothesis in this problem is correct, the probability of a sample of eight recorded jobs averaging less than 44 minutes is less than one percent [Charlie's Productivity]. A. True B. False 29. Using a =0.01, we can conclude that the new workstation facilitates a faster work rate [Workflow Layout]. A. True B. False 30. If the null hypothesis is correct, the probability of getting a sample mean larger than 3 units per hour is .0133 (or 1.33%) [Workflow Layout]. A. True B. False 31. The standard error of the mean for this test is measured in units assembled per hour [Workflow Layout] A. True B. False 32. The model used in this problem is based on twelve treatment levels [MPG-Gas Brands]. A. True B. False 33. The average variation between (or among) treatment means (MSTr) is 84 times larger than the average variation within the samples (MSE) [MPG-Gas Brands]. A. True B. False 34. Testing for equal mean performance, we would reject the null hypothesis at both a = 0.05 and a = 0.01 [MPG-Gas Brands]. A. True B. False 35. From the recorded values, if each individual value from gas Brand-C was 2 mpg more, while that of brand-A was 2 mpg less, it would have no effect on the computed test statistic [MPG-Gas Brands]. A. True B. False 36. There is a significant difference (at a=0.05) in fuel efficiency (as measured by MPG) between Brand- A and Brand-B, but not between Brand-A and Brand-C [MPG-Gas Brands]. A. True B. False37. There is more variance across (or between) groups (SSTr) than there is within the groups (SSE) [Avg. Life-Tire Brands]. A. True B. False 38 There is sufficient evidence (at a=0.05) to reject the null hypothesis [Avg. Life-Tire Brands]. A. True B. False 39 The average variation between treatment groups (MSIr) is greater than the average variation within groups (MSE) [Avg. Life-Tire Brands]. A. True B. False 40 If the last value of Brand C was changed from 25 to 30, while the first value is reduced from 28 to 23, the calculated F value would be smaller [Avg. Life-Tire Brands]. A. True B. False Plot AreaBUSINESS and ECON STATISTICS QUESTIONS - HYPOTHESIS TESTING Schematic Hypothesis Testing - One Mean For X-bar -Use MS Reference San Serif and character code "F7C2" HO: LL = ### S=6 ? {X1, X2,X3 .. Xol? Ha: L = ### x = Ex 6= = 6 / Vn Plot Area # XI C # XIC # XI C # XI C # XI C # XI C # XI C 1= 0 For each Question below, find each of the following items: a. Ho and Ha Value of calculated statistic b. Rejection region. d . Decision and Conclusion[Mean Housing Value] The mean valuation for single-family homes in a large city is assessed (by the county assessor) to be $88,000. Wanting to raise more revenue without raising taxes, a city manager claims the average valuation for homes is too low. On the other side, homeowners believe it is too high. A council member has requested a study to determine if the auditor's average valuation for homes is realistic lie., it could be too high or too lowj. Therefore, a random sample of 36 homes is taken with a computed sample mean of $89,500 and standard deviation of $6,000 [s=$6,000=6). Based on the sample results, what would you tell the council member? Is the county appraiser's claim realistic? Use a = 05. P = $88,000 ? (X1, X2..Xn) P = $88,000 Ho: p = $88,000 i.e., the county assessor's valuation is realistic Ha: p # $88,000 i.e., the county assessor's valuation is not realistic Plot Area Standard Normal Distribution -4.00 -3.00 -2.00 -1.00 0.00 1.00 2.00 3.00 4.00 X Xc X H=88k -1.96- +1.96 Reject Ho --- Reject Ho Hint: =NORM.S.INVID.975)=1.96 Hint: =NORM.S.DIST(1.5,1)=.9332 P-value=1.0000-.9332=.0668 Criterion for decision: Reject Ho if [-1.96 s Zo > +1.96], failed to reject otherwise. Of = 0/vn = $6,000/ 36 = $1,000 Zo = (X - p) / q:= (89,500 - 88,000) / 1000 = 1,500 / 1,000 = +1.50 Decision: Fail to reject Ho Conclusion: At alpha=.05, we fail to reject the county assessor's valuation. There's no need to re-assess.[Cereal Package Filling] A package-filling device is set to fill cereal boxes with a (mean) weight of 20.10 oz of cereal per box. Assume a normal distribution for the fills. The production supervisor suspects that the machine may be over filling the boxes, thereby increasing the material costs. A random sample of 25 boxes is weighed in order to test the claim that the machine is operating, as it should, against the alternative that it is overfilling. The sample mean and standard deviation are 20.13 oz. and 0.05 oz., respectively. Answer the next four questions based on this information. Using a = .01, answer the next four questions on the basis of this information. p $ 20.10oz {X1, XX) p > 20.10 oz Ho: Us 20.10 oz i.e., the machine process is not overfilling H.: ( > 20.10 oz i.e., the machine process is overfilling t-Distribution, 24 DF -4.00 -3.00 -2.00 -1.00 0.00 1.00 2.00 3.00 4.00 J=20.10 oz +2.49 --- Reject H. Criterion for decision: Reject Ho if [Z. > +2.49], failed to reject otherwise. OR = o/Vn = .05/\\25 = .01 oz Plot Area Zo = (X - H) / 02= (20.13 - 20.10) / .01 = .03/.01 = +3.0 Hint: T.INV(0.99,24)=2.49 Hint: =T.DIST(3,24,1)=.9969 =.9969 P-value=1.0000-.9950=.0031 Decision: Reject Ho Conclusion: At alpha=.01, we reject the claim that the machine process is not overfilling. There's a need to re-adjust the machine process. [Chewie-Chocolate Candies] Candies manufactured by Chewie-Chocolate Candies Co. are supposed to weigh at least 2.00 ounces, and they have a standard deviation of 0.10 ounce. Assume a normal distribution for the weights. If a sample of size 100 has an average weight of 1.985 ounces, can we conclude that the average weight is less than 2.00 ounces when testing at a = 0.05. Hint: =NORM.SINV(0.05)=-1.645 Hint: =NORM.S.DIST(-1.5,1)=.0668[Machine Process Specification] A heavy equipment manufacturer produces pistons with mean diameter specification of 20 cm. The quality control manager periodically takes samples to determine if the machine process is operating according to specification. The latest sample of 36 piston revealed a mean of 20.018 cm with a standard deviation of .036 cm. Assume a normal population of diameter lengths. When testing at a=.01, is the machine process meeting specification? p = 20cm ( X1, X2X) ? P = 20cm H.: P = 20.0 cm i.e., the machine process is meeting specification H.: p # 20.0 cm i.e., the machine process is not meeting specification Standard Normal Distribution -4.00 -3.00 -2.00 -1.00 0.00 1.00 2.00 3.00 4.00 J=20cm -2.575- -+2.575 - Reject H. - Reject H. Hint: =NORM.SINVID.995)=2.575 Criterion for decision: Reject Ho if [-2.575 s Z, 2 +2.575], failed to reject otherwise. Ox = ON\ = .036/\\36 = .006 Zo = (X - H) / 62= (20.018 - 20.000) / .006 = .018 / .006 =+3.0 Hint: =NORM.S.DIST(3,1)=.9987 P-value=1.0000-.9987=.0013 Decision: Reject Ho Conclusion: At alpha=.05, we reject the claim that the machine process is meeting specs. There's a need to re-adjust the machine process.[Charlie's Productivity] Charlie's supervisor is not sure if Charlie is eligible for promotion. A worker must have an average time of less than 50 minutes per job if he or she is to be eligible for promotion. Charlie thinks he averages significantly less than 50 minutes for each job and is thus deserving of a promotion. As part of the investigation, the supervisor reviewed the records of nine jobs and recorded the time: 42, 42, 44, 46, 47, 48, 50, 50, and 54 minutes. His average time to complete the nine jobs was x=47 minutes with a standard deviation of =4 minutes. Assume a normal distribution. Using this data, can Charlie justify a claim of averaging under 50 minutes when testing at both o = 0.05 and o = 0.01 level of significance? P 2 50 min. (X1, X26...maxn) ? p
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


