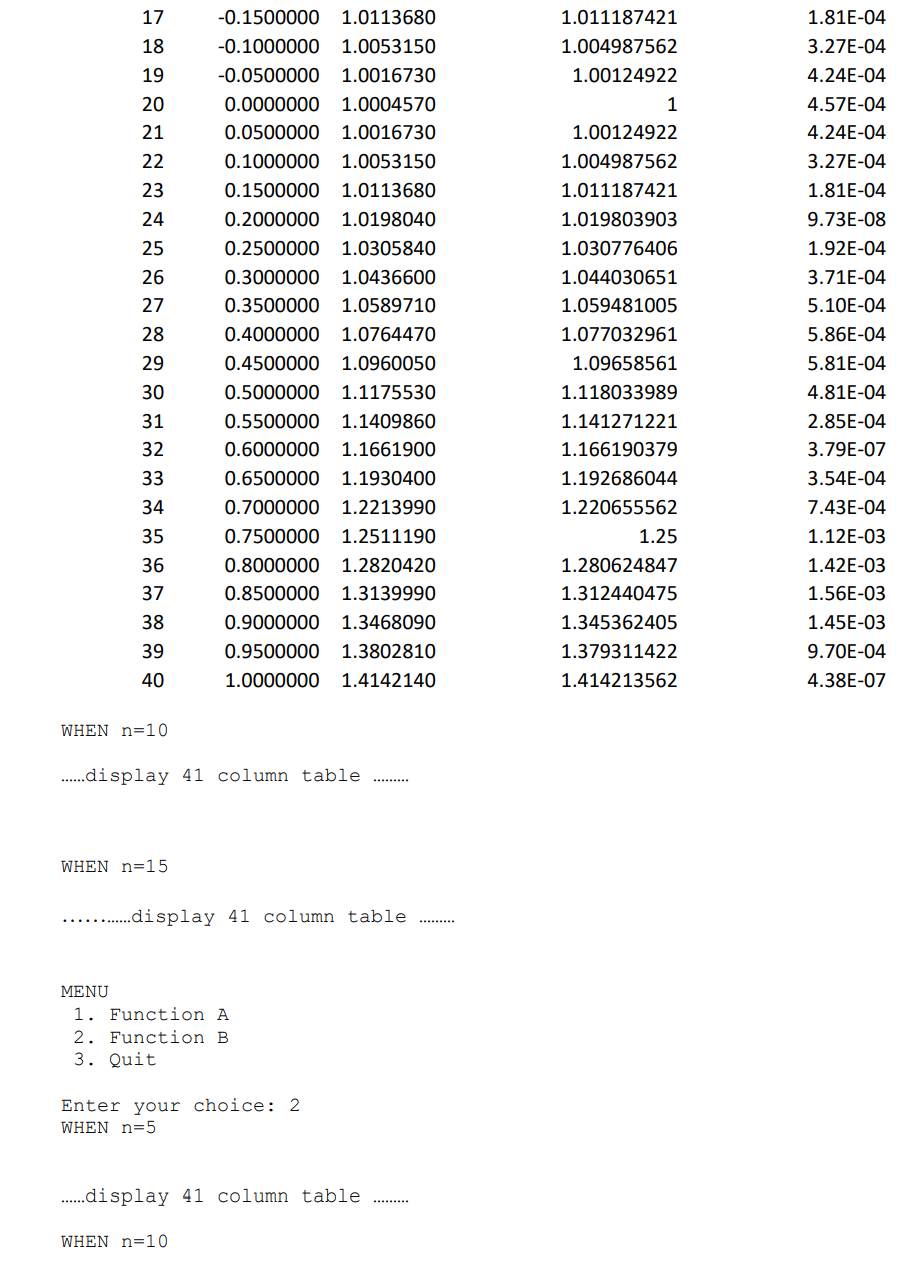
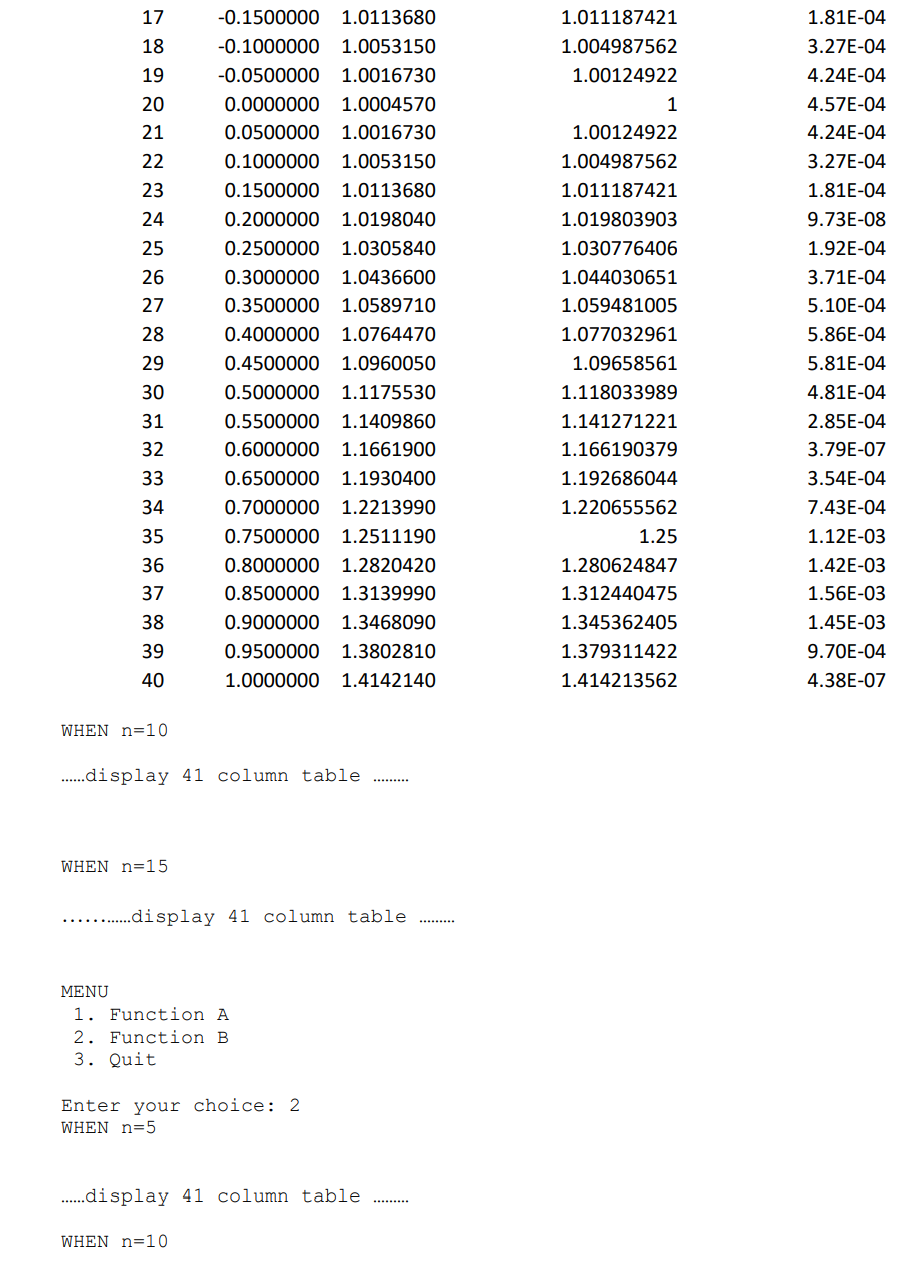
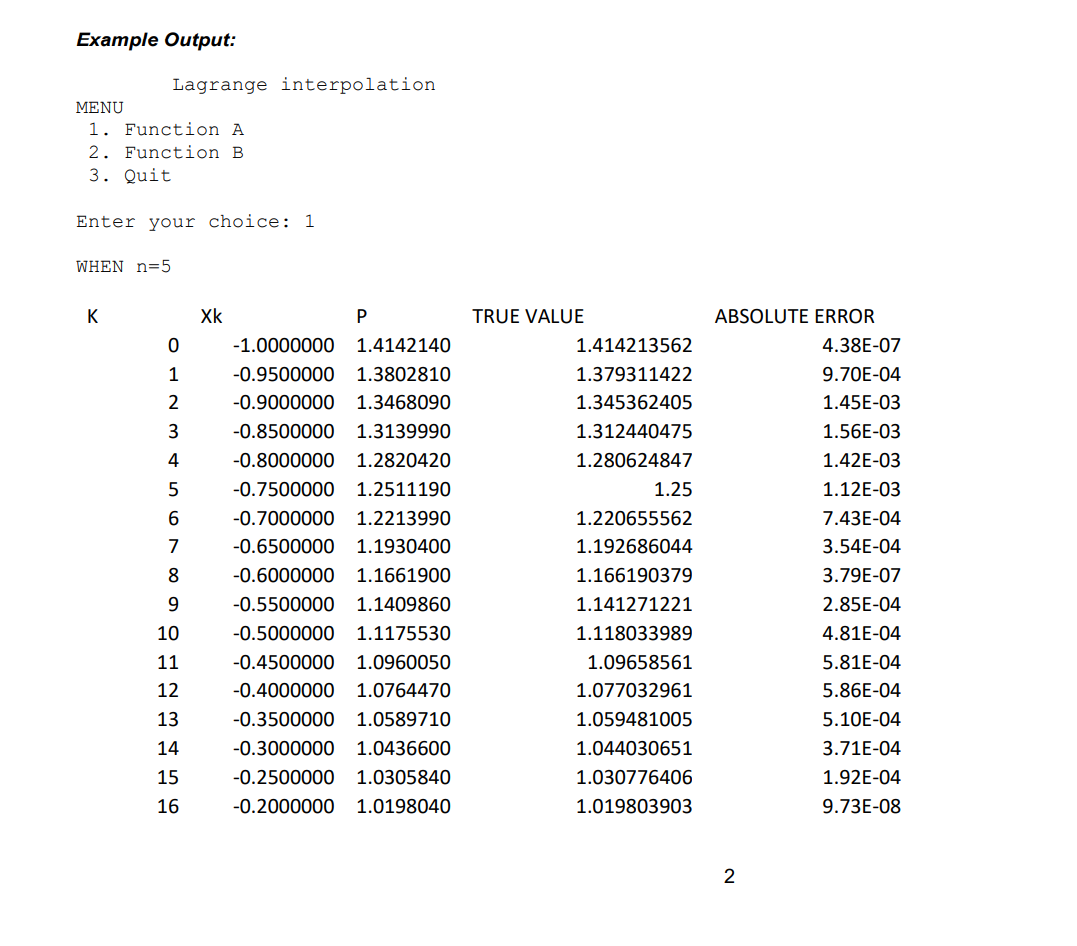
17 18 19 20 21 22 23 24 25 26 27 28 -0.1500000 -0.1000000 -0.0500000 0.0000000 0.0500000 0.1000000 0.1500000 0.2000000 0.2500000 0.3000000 0.3500000 0.4000000 0.4500000 0.5000000 0.5500000 0.6000000 0.6500000 0.7000000 0.7500000 0.8000000 0.8500000 0.9000000 0.9500000 1.0000000 1.0113680 1.0053150 1.0016730 1.0004570 1.0016730 1.0053150 1.0113680 1.0198040 1.0305840 1.0436600 1.0589710 1.0764470 1.0960050 1.1175530 1.1409860 1.1661900 1.1930400 1.2213990 1.2511190 1.2820420 1.3139990 1.3468090 1.3802810 1.4142140 1.011187421 1.004987562 1.00124922 1 1.00124922 1.004987562 1.011187421 1.019803903 1.030776406 1.044030651 1.059481005 1.077032961 1.09658561 1.118033989 1.141271221 1.166190379 1.192686044 1.220655562 1.25 1.280624847 1.312440475 1.345362405 1.379311422 1.414213562 1.81E-04 3.27E-04 4.24E-04 4.57E-04 4.24E-04 3.27E-04 1.81E-04 9.73E-08 1.92E-04 3.71E-04 5.10E-04 5.86E-04 5.81E-04 4.81E-04 2.85E-04 3.79E-07 3.54E-04 7.43E-04 1.12E-03 1.42E-03 1.56E-03 1.45E-03 9.70E-04 4.38E-07 29 30 31 32 33 34 35 36 37 38 39 40 WHEN n=10 ......display 41 column table WHEN n=15 ........ display 41 column table ........ MENU 1. Function A 2. Function B 3. Quit Enter your choice: 2 WHEN n=5 ......display 41 column table WHEN n=10 17 18 19 20 21 22 23 24 25 26 27 28 -0.1500000 -0.1000000 -0.0500000 0.0000000 0.0500000 0.1000000 0.1500000 0.2000000 0.2500000 0.3000000 0.3500000 0.4000000 0.4500000 0.5000000 0.5500000 0.6000000 0.6500000 0.7000000 0.7500000 0.8000000 0.8500000 0.9000000 0.9500000 1.0000000 1.0113680 1.0053150 1.0016730 1.0004570 1.0016730 1.0053150 1.0113680 1.0198040 1.0305840 1.0436600 1.0589710 1.0764470 1.0960050 1.1175530 1.1409860 1.1661900 1.1930400 1.2213990 1.2511190 1.2820420 1.3139990 1.3468090 1.3802810 1.4142140 1.011187421 1.004987562 1.00124922 1 1.00124922 1.004987562 1.011187421 1.019803903 1.030776406 1.044030651 1.059481005 1.077032961 1.09658561 1.118033989 1.141271221 1.166190379 1.192686044 1.220655562 1.25 1.280624847 1.312440475 1.345362405 1.379311422 1.414213562 1.81E-04 3.27E-04 4.24E-04 4.57E-04 4.24E-04 3.27E-04 1.81E-04 9.73E-08 1.92E-04 3.71E-04 5.10E-04 5.86E-04 5.81E-04 4.81E-04 2.85E-04 3.79E-07 3.54E-04 7.43E-04 1.12E-03 1.42E-03 1.56E-03 1.45E-03 9.70E-04 4.38E-07 29 30 31 32 33 34 35 36 37 38 39 40 WHEN n=10 ......display 41 column table WHEN n=15 ........ display 41 column table ........ MENU 1. Function A 2. Function B 3. Quit Enter your choice: 2 WHEN n=5 ......display 41 column table WHEN n=10 NOTE: Plan to finish a few days early to avoid last minute hardware/software or other unexpected holdups, for which no allowance is given. NOTE: The code in this assignment must be your own work. It must not be code taken from another student or written for you by someone else, even if you give a reference to the person you got it from (attribution); if it is not entirely your own work it will be treated as plagiarism and given a fail mark, or less. Problem Description: Use Lagrange interpolation to interpolate the following functions: (a) f(x) = V1 + x2 1 (b) f(x) = 1+25x2 using a set of n+1 regularly spaced nodes computed by the following equation: 2(k 1) k = 1,2,3,... ..., n + 1 Xk = -1+ n Test your generated polynomial with different orders, n= 5, 10, 20 and compute the interpolation polynomial Pn(x) at 41 regularly spaced points. For each value of xk the Lagrange polynomial approximation is output together with the exact /true value from the math library, also output the absolute error. What to Submit: Set up an empty project in Visual Studio 2019 with the name ass1. add a new source code file ass1.cpp\c to the project and write your code in it to implement the application, as described above. Then on Brightspace in the Assignment Submission folder submit your ass1.cpp\c file. Don't submit the project, submit only .cor.cpp file. Example Output: Lagrange interpolation MENU 1. Function A 2. Function B 3. Quit Enter your choice: 1 WHEN n=5 K 0 1 2 3 4 5 6 7 Xk -1.0000000 -0.9500000 -0.9000000 -0.8500000 -0.8000000 -0.7500000 -0.7000000 -0.6500000 -0.6000000 -0.5500000 -0.5000000 -0.4500000 -0.4000000 -0.3500000 -0.3000000 -0.2500000 -0.2000000 P 1.4142140 1.3802810 1.3468090 1.3139990 1.2820420 1.2511190 1.2213990 1.1930400 1.1661900 1.1409860 1.1175530 1.0960050 1.0764470 1.0589710 1.0436600 1.0305840 1.0198040 TRUE VALUE 1.414213562 1.379311422 1.345362405 1.312440475 1.280624847 1.25 1.220655562 1.192686044 1.166190379 1.141271221 1.118033989 1.09658561 1.077032961 1.059481005 1.044030651 1.030776406 1.019803903 ABSOLUTE ERROR 4.38E-07 9.70E-04 1.45E-03 1.56E-03 1.42E-03 1.12E-03 7.43E-04 3.54E-04 3.79E-07 2.85E-04 4.81E-04 5.81E-04 5.86E-04 5.10E-04 3.71E-04 1.92E-04 9.73E-08 8 9 10 11 12 13 14 15 16 2 17 18 19 20 21 22 23 24 25 26 27 28 -0.1500000 -0.1000000 -0.0500000 0.0000000 0.0500000 0.1000000 0.1500000 0.2000000 0.2500000 0.3000000 0.3500000 0.4000000 0.4500000 0.5000000 0.5500000 0.6000000 0.6500000 0.7000000 0.7500000 0.8000000 0.8500000 0.9000000 0.9500000 1.0000000 1.0113680 1.0053150 1.0016730 1.0004570 1.0016730 1.0053150 1.0113680 1.0198040 1.0305840 1.0436600 1.0589710 1.0764470 1.0960050 1.1175530 1.1409860 1.1661900 1.1930400 1.2213990 1.2511190 1.2820420 1.3139990 1.3468090 1.3802810 1.4142140 1.011187421 1.004987562 1.00124922 1 1.00124922 1.004987562 1.011187421 1.019803903 1.030776406 1.044030651 1.059481005 1.077032961 1.09658561 1.118033989 1.141271221 1.166190379 1.192686044 1.220655562 1.25 1.280624847 1.312440475 1.345362405 1.379311422 1.414213562 1.81E-04 3.27E-04 4.24E-04 4.57E-04 4.24E-04 3.27E-04 1.81E-04 9.73E-08 1.92E-04 3.71E-04 5.10E-04 5.86E-04 5.81E-04 4.81E-04 2.85E-04 3.79E-07 3.54E-04 7.43E-04 1.12E-03 1.42E-03 1.56E-03 1.45E-03 9.70E-04 4.38E-07 29 30 31 32 33 34 35 36 37 38 39 40 WHEN n=10 ......display 41 column table WHEN n=15 ........ display 41 column table ........ MENU 1. Function A 2. Function B 3. Quit Enter your choice: 2 WHEN n=5 ......display 41 column table WHEN n=10 17 18 19 20 21 22 23 24 25 26 27 28 -0.1500000 -0.1000000 -0.0500000 0.0000000 0.0500000 0.1000000 0.1500000 0.2000000 0.2500000 0.3000000 0.3500000 0.4000000 0.4500000 0.5000000 0.5500000 0.6000000 0.6500000 0.7000000 0.7500000 0.8000000 0.8500000 0.9000000 0.9500000 1.0000000 1.0113680 1.0053150 1.0016730 1.0004570 1.0016730 1.0053150 1.0113680 1.0198040 1.0305840 1.0436600 1.0589710 1.0764470 1.0960050 1.1175530 1.1409860 1.1661900 1.1930400 1.2213990 1.2511190 1.2820420 1.3139990 1.3468090 1.3802810 1.4142140 1.011187421 1.004987562 1.00124922 1 1.00124922 1.004987562 1.011187421 1.019803903 1.030776406 1.044030651 1.059481005 1.077032961 1.09658561 1.118033989 1.141271221 1.166190379 1.192686044 1.220655562 1.25 1.280624847 1.312440475 1.345362405 1.379311422 1.414213562 1.81E-04 3.27E-04 4.24E-04 4.57E-04 4.24E-04 3.27E-04 1.81E-04 9.73E-08 1.92E-04 3.71E-04 5.10E-04 5.86E-04 5.81E-04 4.81E-04 2.85E-04 3.79E-07 3.54E-04 7.43E-04 1.12E-03 1.42E-03 1.56E-03 1.45E-03 9.70E-04 4.38E-07 29 30 31 32 33 34 35 36 37 38 39 40 WHEN n=10 ......display 41 column table WHEN n=15 ........ display 41 column table ........ MENU 1. Function A 2. Function B 3. Quit Enter your choice: 2 WHEN n=5 ......display 41 column table WHEN n=10 NOTE: Plan to finish a few days early to avoid last minute hardware/software or other unexpected holdups, for which no allowance is given. NOTE: The code in this assignment must be your own work. It must not be code taken from another student or written for you by someone else, even if you give a reference to the person you got it from (attribution); if it is not entirely your own work it will be treated as plagiarism and given a fail mark, or less. Problem Description: Use Lagrange interpolation to interpolate the following functions: (a) f(x) = V1 + x2 1 (b) f(x) = 1+25x2 using a set of n+1 regularly spaced nodes computed by the following equation: 2(k 1) k = 1,2,3,... ..., n + 1 Xk = -1+ n Test your generated polynomial with different orders, n= 5, 10, 20 and compute the interpolation polynomial Pn(x) at 41 regularly spaced points. For each value of xk the Lagrange polynomial approximation is output together with the exact /true value from the math library, also output the absolute error. What to Submit: Set up an empty project in Visual Studio 2019 with the name ass1. add a new source code file ass1.cpp\c to the project and write your code in it to implement the application, as described above. Then on Brightspace in the Assignment Submission folder submit your ass1.cpp\c file. Don't submit the project, submit only .cor.cpp file. Example Output: Lagrange interpolation MENU 1. Function A 2. Function B 3. Quit Enter your choice: 1 WHEN n=5 K 0 1 2 3 4 5 6 7 Xk -1.0000000 -0.9500000 -0.9000000 -0.8500000 -0.8000000 -0.7500000 -0.7000000 -0.6500000 -0.6000000 -0.5500000 -0.5000000 -0.4500000 -0.4000000 -0.3500000 -0.3000000 -0.2500000 -0.2000000 P 1.4142140 1.3802810 1.3468090 1.3139990 1.2820420 1.2511190 1.2213990 1.1930400 1.1661900 1.1409860 1.1175530 1.0960050 1.0764470 1.0589710 1.0436600 1.0305840 1.0198040 TRUE VALUE 1.414213562 1.379311422 1.345362405 1.312440475 1.280624847 1.25 1.220655562 1.192686044 1.166190379 1.141271221 1.118033989 1.09658561 1.077032961 1.059481005 1.044030651 1.030776406 1.019803903 ABSOLUTE ERROR 4.38E-07 9.70E-04 1.45E-03 1.56E-03 1.42E-03 1.12E-03 7.43E-04 3.54E-04 3.79E-07 2.85E-04 4.81E-04 5.81E-04 5.86E-04 5.10E-04 3.71E-04 1.92E-04 9.73E-08 8 9 10 11 12 13 14 15 16 2