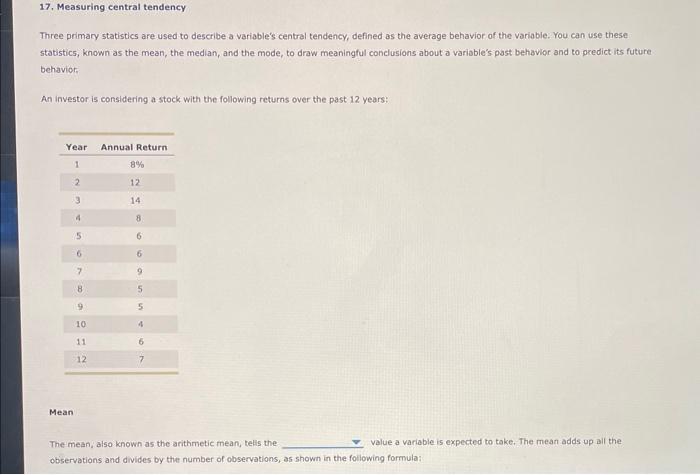
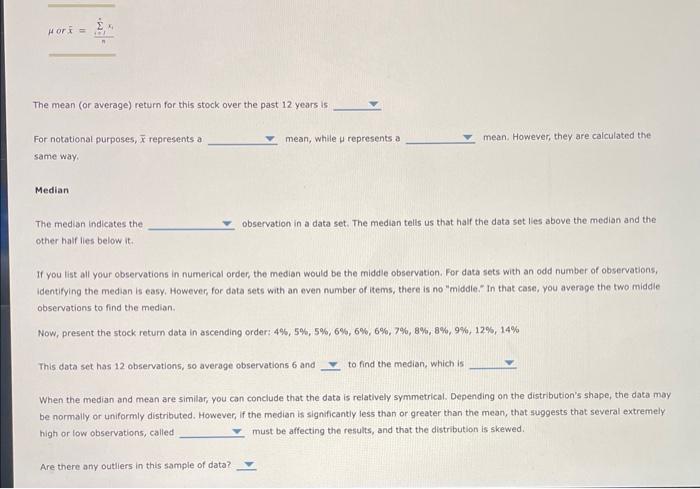
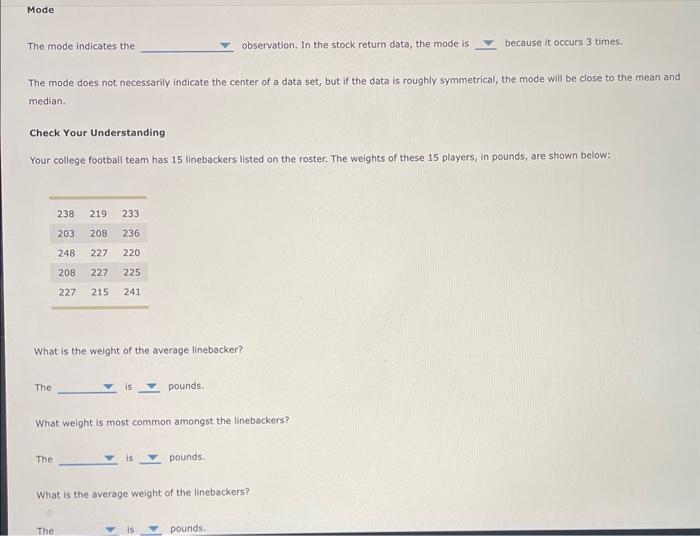
17. Measuring central tendency Three primary statistics are used to describe a variable's central tendency, defined as the average behavior of the variable. You can use these statistics, known as the mean, the median, and the mode, to draw meaningful conclusions about a variable's past behavior and to predict its future behavior: An investor is considering a stock with the following returns over the past 12 years: Mean The mean; also known as the arithmetic mean, kells the value a variable is expected to take. The mean adds up all the observations and divides by the number of observations, as shown in the following formula: orx=n^jx1 The mean (or average) return for this stock over the past 12 years is For notational purposes, x represents a mean, while represents a mean. However, they are calculated the same way, Median The median indicates the observation in a data set. The median tells us that half the data set lies above the median and the other half lies below it. If you list all your observations in numerical order, the median would be the middle observation. For data sets with an odd number of observations, identifying the median is easy. However, for data sets with an even number of items, there is no "middle." In that case. You average the two middle. observations to find the median. Now, present the stock retum data in ascending order: 4%,5%,5%,6%,6%,6%,7%,8%,8%,9%,12%,14%. This data set has 12 observations, 50 average observations 6 and to find the median, which is When the median and mean are similar, you can conclude that the data is relatively symmetrical. Depending on the distribution's shape, the data may be normally or uniformly distributed. However, if the median is significantly less than or greater than the mean, that suggests that several extremely high or low observations, called must be affecting the results, and that the distribution is skewed. Are there any outliers in this sample of data? The mode indicates the observation. In the stock return data, the mode is because it occurs 3 times. The mode does not necessarily indicate the center of a data set, but if the data is roughly symmetrical, the mode will be ciose to the mean and median. Check Your Understanding Your college football team has 15 linebackers listed on the roster. The weights of these 15 piayers, in pounds, are shown below: What is the weight of the average linebacker? The is pounds, What weight is most common amongst the linebackers? The is. pounds. What is the average weight of the linebackers