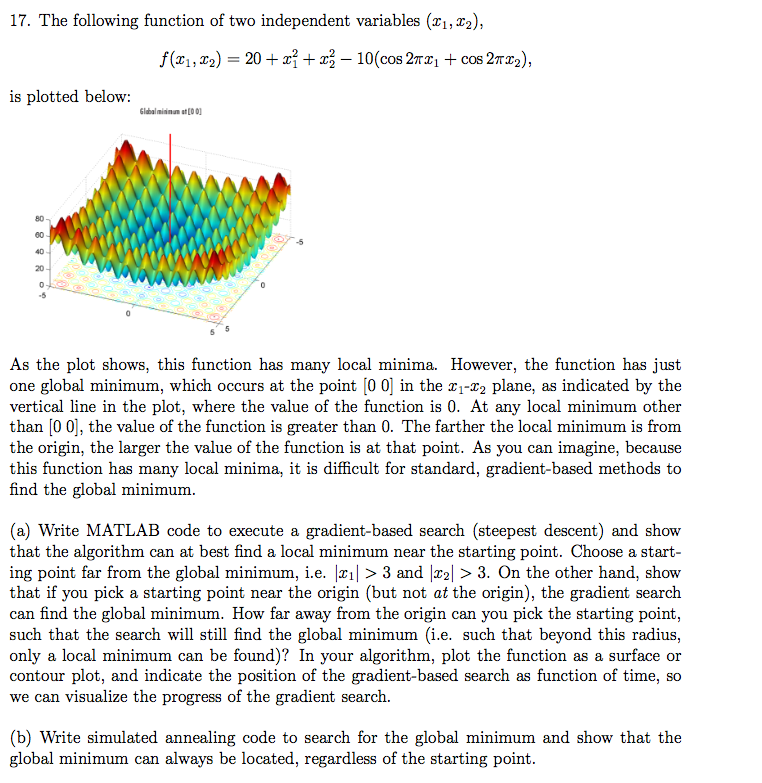
17. The following function of two independent variables (x,2), is plotted below: labalnianam at[O 0 80 20- As the plot shows, this function has many local minima. However, the function has just one global minimum, which occurs at the point [0 0] in the x1-T2 plane, as indicated by the vertical line in the plot, where the value of the function is 0. At any local minimum other than 10 0], the value of the function is greater than 0. The farther the local minimum is from the origin, the larger the value of the function is at that point. As you can imagine, because this function has many local minima, it is difficult for standard, gradient-based methods to find the global minimum. (a) Write MATLAB code to execute a gradient-based search (steepest descent) and show that the algorithm can at best find a local minimum near the starting point. Choose a start ing point far from the global minimum, i.e. |T1| > 3 and > 3. On the other hand, show that if you pick a starting point near the origin (but not at the origin), the gradient search can find the global minimum. How far away from the origin can you pick the starting point, such that the search will still find the global minimum (i.e. such that beyond this radius, only a local minimum can be found)? In your algorithm, plot the function as a surface or contour plot, and indicate the position of the gradient-based search as function of time, so we can visualize the progress of the gradient search. (b) Write simulated annealing code to search for the global minimum and show that the global minimum can always be located, regardless of the starting point 17. The following function of two independent variables (x,2), is plotted below: labalnianam at[O 0 80 20- As the plot shows, this function has many local minima. However, the function has just one global minimum, which occurs at the point [0 0] in the x1-T2 plane, as indicated by the vertical line in the plot, where the value of the function is 0. At any local minimum other than 10 0], the value of the function is greater than 0. The farther the local minimum is from the origin, the larger the value of the function is at that point. As you can imagine, because this function has many local minima, it is difficult for standard, gradient-based methods to find the global minimum. (a) Write MATLAB code to execute a gradient-based search (steepest descent) and show that the algorithm can at best find a local minimum near the starting point. Choose a start ing point far from the global minimum, i.e. |T1| > 3 and > 3. On the other hand, show that if you pick a starting point near the origin (but not at the origin), the gradient search can find the global minimum. How far away from the origin can you pick the starting point, such that the search will still find the global minimum (i.e. such that beyond this radius, only a local minimum can be found)? In your algorithm, plot the function as a surface or contour plot, and indicate the position of the gradient-based search as function of time, so we can visualize the progress of the gradient search. (b) Write simulated annealing code to search for the global minimum and show that the global minimum can always be located, regardless of the starting point







