1Background

Let G = (V,E) be a simple, unweighted, undirected graph. The distance between two vertices u,v V , given by d(u,v), is defined as the length of the shortest path between u and v in the graph G. Note that d(u,u) = 0.

The farness of a vertex u in a graph G is defined as:

far(u) = ^Xd(u,v)

vV

The closeness centrality of u is then defined as:

1 C_C(u) = _____far(u)

2Problem

This year during Dragon Con, Batgirl made a special visit to Klaus to visit your professor. She has an urgent problem and needs theoretical and computational help before September 13. She received a tip-off that the Riddler is going to perform a major heist in Gotham City at some point during the following weekBatgirl is planning on preventing it and saving the city.

More specifically, Batgirl does not know when or where exactly the heist will occur, so she wants to find a well located position in the city. She plans on remaining at that position and since it is well located, at the first sign of the heist she can quickly move to the correct location and prevent it. There are a number of points of interest that she has identified that the heist may occur at. Closeness centrality seems like an important tool as she is looking for a ranking of locations that are the least far from every point a heist may occur at.

Your TAs have been working hard helping Batman connect his cell phone audio player to bluetooth on his batmobile, so we are turning to you for help with this problem.

You should approach the problem in the following way. You will be given a connected graph G (for Batgirls problem, this will consist of the intersections as vertices and roads as edges throughout Gotham City) and a set of vertices H (the intersections the heist may occur at). Let the heistcloseness centrality of u be given by the following:

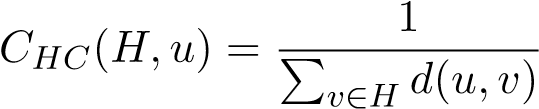
(1)

Your job is to design, analyze, and implement an algorithm to efficiently compute the heist-closeness centrality for each vertex in a graph.

Concretely, you need to do the following:

1.Design an algorithm to compute the heist-closeness centrality, as defined by (1). Write thehigh-level idea, then concrete details and pseudo-code for the algorithm.

2.Prove the feasibility of the algorithm. That is, prove that the algorithm will correctly computethe heist-closeness centrality for each vertex.

3.Compute and prove the run-time and space complexity of the algorithm. Identify if differentdata structures will impact the complexity.

4.Using one of the provided templates, implement your new algorithm and ensure it runscorrectly on the sample graphs provided.

5.Describe your implementation in writing and perform an evaluation that includes a plotcontaining the run-time as the number of edges increase. Describe at a high level how different input graph topologies may impact your run-time.

3I/O File Formats

There are three file formats used for this assignment which are described in this section.

3.1Graph File Format

The input graph files are in a format that is easy to construct a CSR from. The file extension used is .graph. The format is as follows:

n m

s1 d1

s2 d2

...

sm dm

Here, n is n = |V | as expected. Due to the design of CSR construction in the templates, m is actually 2m = 2|E|, with each edge essentially considered as two directed edges with each direction included in the input file. The values should be formatted as ASCII integers.

The edges must be sorted numerically by source.

3.2Heist Nodes File Format

The file extension .h is used for heist nodes. The heist nodes are provided in the following format:

k

v1

v2

...

vk

Here, k is the number of heist nodes, or k = |H|. Each following vi is a given vertex ID that is a heist node. The values should be formatted as ASCII integers.

3.3Output File Format

The output file format has an extension of .hc and is as follows:

n

v1-hcc

v2-hcc

...

vn-hcc

Here, n is n = |V |, as in the input graph format. Each following line corresponds to the respective vertexs computed C_HC value. The values should be formatted as an ASCII integer and doubles respectively.

4Submission Instructions

Please follow these instructions carefully.

You should submit two files:

A PDF containing your typed written assignment: the algorithm, the feasibility proof,the run-time and space complexity analysis and proof, and the implementation report and evaluation.

A single source code file (C++, Python, or Java) that implements your algorithm andcompiles or runs in the templates provided at https://github.gatech.edu/ucatalyurek7/cse6140-Fall18.git. This file will be used to replace hcc.cpp, HCC.java, or hcc.py appropriately when testing

Your code should contain no dependencies beyond what the templates contain (standard libraries are okay) and should compile or run on a vanilla installation of Ubuntu 18.04 with only build-essential, default-jdk, python3, and python2.7 installed. If you have any doubt about whether it will compile or run, please reach out to the TAs before the deadline.

CHC(H,u) = CHC(H,u) =