1.Describe in detail how H in Theorem 12.1 can be modified to produce H.

There does not exist any Turing machine H that behaves as required by Definition 12.1. The halting problem is

therefore undecidable.

Proof: We assume the contrary, namely, that there exists an algorithm, and consequently some Turing machine H, that

solves the halting problem. The input to H will be the string wMw. The requirement is then that, given any wM w, the

Turing machine Hwill halt with either a yes or no answer. We achieve this by asking that H halt in one of two

corresponding final states, say, qy or qn. The situation can be visualized by a block diagram like Figure 12.1. The intent

of this diagram is to indicate that, if H is started in state q0 with input wM w, it will eventually halt in state qy or qn. As

required by Definition 12.1, we want H to operate according to the following rules:

q0wMw*Hx1qyx2q0wMw*Hx1qyx2

if M applied to w halts, and

q0wMw*Hy1qny2q0wMw*Hy1qny2

if M applied to w does not halt.

Next, we modify H to produce a Turing machine H with the structure shown in Figure 12.2. With the added states

in Figure 12.2 we want to convey that the transitions between state qy and the new states qa and qb are to be made,

regardless of the tape symbol, in such a way that the tape remains unchanged. The way this is done is straightforward.

Comparing H and H we see that, in situations where H reaches qy and halts, the modified machine H will enter an

infinite loop. Formally, the action of H is described by

FIGURE 12.1

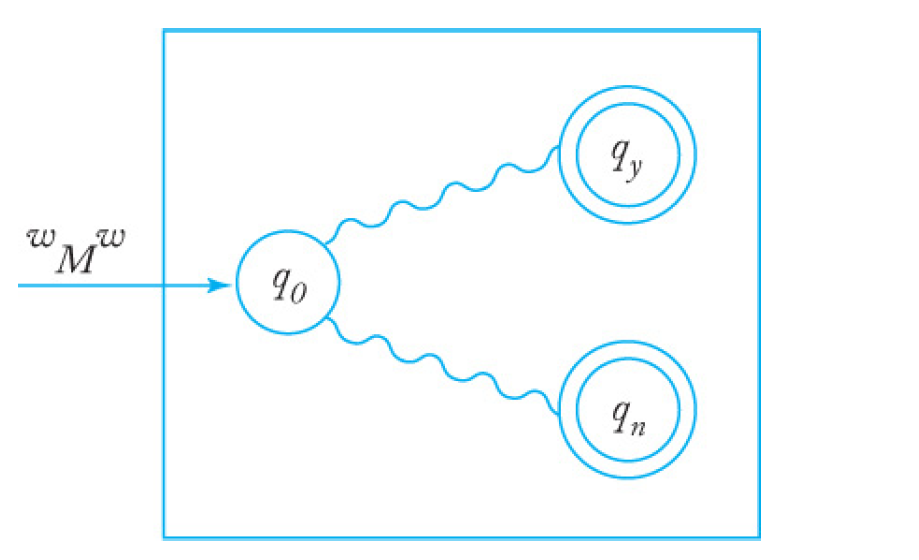
FIGURE 12.2

q0wMw*H'q0wMw*H

if M applied to w halts, and

q0wMw*H'y1qny2q0wMw*Hy1qny2

if M applied to w does not halt.

From H we construct another Turing machine HH^. This new machine takes as input wMand copies it, ending in its

initial state q0. After that, it behaves exactly like H. Then the action of HH^ is such that

q0wM*H q0wMwM*H q0wM*H^ q0wMwM*H^

if M applied to wM halts, and

q0wM*H q0wMwM*H y1qny2q0wM*H^ q0wMwM*H^ y1qny2

if M applied to wM does not halt.

Now HH^ is a Turing machine, so it has a description in {0, 1}*, say, ww^. This string, in addition to being the

description of HH^, also can be used as input string. We can therefore legitimately ask what would happen if HH^ is

applied to ww^. From the above, identifying M with HH^, we get

q0w*H q0w^*H^

if HH^ applied to ww^ halts, and

q0w*H y1qny2q0w^*H^ y1qny2

if HH^ applied to ww^ does not halt. This is clearly nonsense. The contradiction tells us that our assumption of the

existence of H, and hence the assumption of the decidability of the halting problem, must be false.

One may object to Definition 12.1, since we required that, to solve the halting problem, H had to start and

end in very specific configurations. It is, however, not hard to see that these somewhat arbitrarily chosen

conditions play only a minor role in the argument, and that essentially the same reasoning could be used

with any other starting and ending configurations. We have tied the problem to a specific definition for the

sake of the discussion, but this does not affect the conclusion.

It is important to keep in mind what Theorem 12.1 says. It does not preclude solving the halting problem for

specific cases; often we can tell by an analysis of M and w whether or not the Turing machine will halt. What

the theorem says is that this cannot always be done; there is no algorithm that can make a correct decision

for all wM and w.

The arguments for proving Theorem 12.1 were given because they are classical and of historical interest. The

conclusion of the theorem is actually implied in previous results as the following argument shows.

2. In the general halting problem, we ask for an algorithm that gives the correct answer for any M and w. We

can relax this generality, for example, by looking for an algorithm that works for all M but only a single w.

We say that such a problem is decidable if for every wthere exists a (possibly different) algorithm that

determines whether or not (M, w) halts. Show that even in this restricted setting the problem is undecidable.