$2\mathrm{.}1$ Distance traveled by a robot

We can estimate the total distance traveled by a robot by adding up the

distances between consecutive points on the trajectory of the robot. Here,

we only consider the x and y state variables but not the state variabe of

the robot. Given two consecutive points $($x$1,$ y$1)$ and $($x$2,$ y$2),$ their distance

is defined as d$(($x$1,$ y$1),($x$2,$ y$2))=$ sqrt$($x$1-$x$2)^2+($y$1-$y$2)^2).$ If a robot traveled through a sequence of points: $($x$0,$ y$0),($x$1,$ y$1),($x$2,$ y$2),...,($xN $,$ yN $)$;

then the total distance that it traveled can be estimated as:

N

X$1$

k$=0$

d$(($xk$,$ yk$),($xk$+1,$ yk$+1))=$ d$(($x$0,$ y$0),($x$1,$ y$1))+$d$(($x$1,$ y$1),($x$2,$ y$2))++$d$(($xN$1,$ yN$1),($xN $,$ yN $))$

Examples:

The distance between the two points $(0,1)$ and $(4,2)$ is d$((0,1),(4,2))=$

sqrt$((04)^2+(1(2))^2)=25=5$ meters.

If a robot traveled through $4$ points: $(0,0)$ to $(0\mathrm{.}5,0\mathrm{.}7)$ to $(0\mathrm{.}6,0\mathrm{.}9)$ to

$(1\mathrm{.}0,1\mathrm{.}1)$; then its total travel distance is:

d$((0,0),(0\mathrm{.}5,0\mathrm{.}7))+$ d$((0\mathrm{.}5,0\mathrm{.}7),(0\mathrm{.}6,0\mathrm{.}9))+$ d$((0\mathrm{.}6,0\mathrm{.}9),(1\mathrm{.}0,1\mathrm{.}1))=0\mathrm{.}86+0\mathrm{.}05+0\mathrm{.}2=1\mathrm{.}11$ meters

$2\mathrm{.}2$ Tasks

Write a C program as follows:

$1.$ It defines a new structure type $($with typedef$)$ named RobotState

that has $3$ double members: x$,$ y$,$ and theta. A structure of this

RobotState type represents a state of a robot.

$2.$ It defines a new structure type $($with typedef$)$ named RobotControl

that has $2$ double members: v and w$.$ A structure of this RobotControl

type represents two control inputs v and w of a robot.

$3.$ It defines a function named robot$()$ with the following prototype:

RobotState robot$($double T$,$ RobotState s$,$ RobotControl ctrl$)$;

The function robot$()$ takes a discretization period T$,$ the current robot's

state s of type RobotState, and the current control inputs ctrl of

type RobotControl, to calculate and return as the function's output

the next robot state of type RobotState $($that$\text{'}$s the return value of

the function$).$ The function robot$()$ can be used as in the following

example:

RobotState current $=\{0\mathrm{.}0,0\mathrm{.}0,0\mathrm{.}0\}$; $/*$ x$,$ y$,$ theta $*/$

RobotControl u $=\{0\mathrm{.}5,0\mathrm{.}1\}$; $/*$ v$,$ w $*/$

RobotState next;

next $=$ robot$(0\mathrm{.}1,$ current, u$)$; $/*$ Next state $*/$

Upon execution of the example code, by applying the robot's equations

in the previous section, the next robot state is $($x $=0\mathrm{.}05,$ y $=0\mathrm{.}0,$ $=$

$0\mathrm{.}01).$

Hint: do not directly check whether a floating$-$point number equals

$0\mathrm{.}0$; instead, compare its absolute value to a small number, such as

$1$e$-9.$

if $($fabs$($s$.$w$)<mtext></mtext><mn>1</mn>$e$-9)\{$

$//$ w can be considered zero

$\}$

else $\{$

$//$ w can be considered non$-$zero

$\}$

It definnes a function named distance$()$ with the following prototype:

double distance$($RobotState s$1,$ RobotState s$2)$;

The function distance$()$ takes two consecutive robot states s$1$ and s$2$

and calculates and returns the distance between them $($as the function's

return value$).$

The main function $/$ program does the following:

$-$ It reads from input the data and control sequences for possibly

several robots. The input has the following format:

robot

T$1$ x$1\_0$ y$1\_0$ theta$1\_0$

v$1\_0$ w$1\_0$

v$1\_1$ w$1\_1$

$...$

robot

T$2$ x$2\_0$ y$2\_0$ theta$2\_0$

v$2\_0$ w$2\_0$

v$2\_1$ w$2\_1$

Explanation:

$-$ The data for each robot begins with the string "robot $"$ followed by the name of the robot.

$-$ After that, the next line contains four floating$-$point numbers,

which are respectively the discretization period T and the

initial state x$(0),$ y$(0),$ and $(0)$ of that robot.

$-$ After that, the subsequent lines dene the sequence of control

input pairs $($v$($k$),$ w$($k$))$ for the robot, starting with k $=0,$

one pair on each line. For example, the first pair are v$(0)$ and

w$(0)$; the next pair on the next line are v$(1)$ and w$(1)$; and

so on$.$

$-$ The control sequence for the robot ends when a new robot

starts $($with the line "robot $...")$ or when there is no more

input. The length of the control sequence is not known in

advance.

You can assume that each line of input will not exceed $80$ characters and that there are no more than $5$ robots dened in the

input. See the next subsection "Hints" for some hints on how to

process the input format.

Given the above data of possibly multiple robots read from the

input, the main program simulates the movement of each robot

$($similar to Phase $1),$ using the robot$()$ function. For each robot,

the program must calculate and store the following values: its

name, its initial state, its nal state, its final time $($k $$ T in

seconds$),$ and the total distance that it traveled. $```$

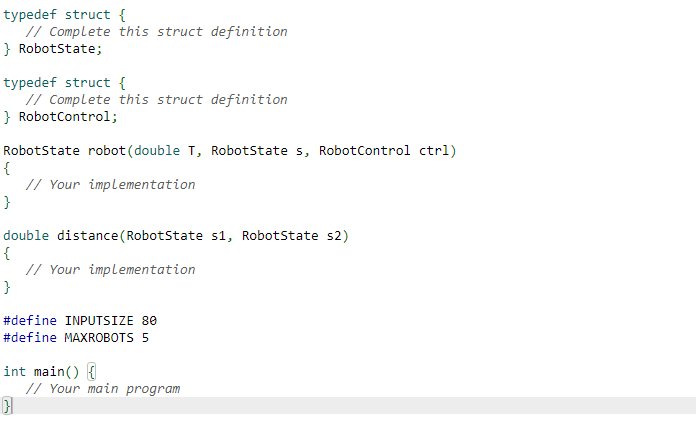
typedef struct $\{$

$//$ Complete this struct definition

$\}$ RobotState;

typedef struct $\{$

$//$ Complete this struct definition

$\}$ RobotControl;

RobotState robot$($double T$,$ RobotState s$,$ RobotControl ctrl$)$

$\{$

$//$ Your implementation

$\}$

double distance$($RobotState s$1,$ RobotState s$2)$

$\{$

$//$ Your implementation

$\}$

#define INPUTSIZE $80$

#define MAXROBOTS $5$

int main$()\{$

$//$ Your main program

$\}$

$```$ Example: If the input is

$```$

robot Opportunity

$0\mathrm{.}1000$

$1\mathrm{.}00\mathrm{.}5$

$1\mathrm{.}51\mathrm{.}0$

$1\mathrm{.}21\mathrm{.}5$

$0\mathrm{.}81\mathrm{.}5$

robot Curiosity

$0\mathrm{.}1000\mathrm{.}5$

$0\mathrm{.}320\mathrm{.}32$

$0\mathrm{.}210\mathrm{.}31$

$0\mathrm{.}20\mathrm{.}59$

$0\mathrm{.}350\mathrm{.}05$

$0\mathrm{.}240\mathrm{.}21$

$```$

then the output is

Number of robots: $2$

Robot Opportunity h