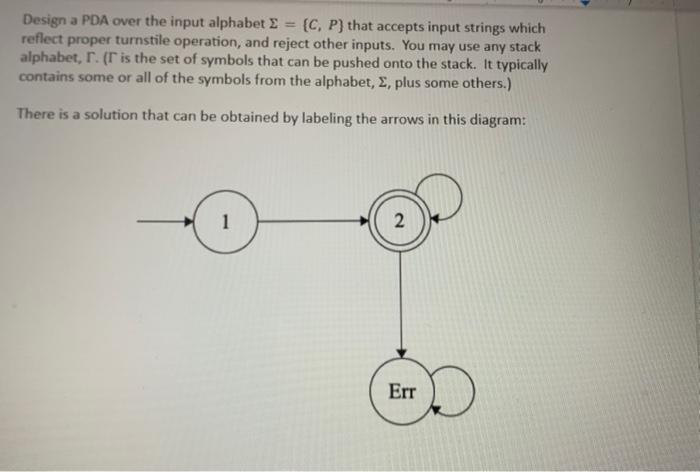
2. (20 points) Consider a turnstile like we did in the first lecture of the course. Assume it is coin operated, and an intern at the company that makes it is given the following task: Sit in a subway station where these machines are in use. Wotch one of them all day, from its initial power-on at 5 am until powerdown at midnight. Write down a symbol for each of the following observed events in the order they occur: C for: "coin goes in", and "p" for "person passes through". Proper turnstile operation: - The power-on state is tocked. - Dropping in a coin stores the coin and puts the turnstile in the unlocked state. - A person cannot Pass when the turnstile is locked. - Passing through the turnstile moves it to the locked state, and consumes a stored coin. - The turnstile allows a person to drop in as many coins as they want, and these will each be stored and used to pay for subsequent subway passengers. - At the end of the day, there may be unused coins stored in the turnstile. Observing a properly working turnstile, the intern might record, e.g. C,P,C,C,P,P // The second person paid for the one behind them/ C,C,C,C,P // The first person for 3 more people, but none showed A faulty turnstile would allow someone through without payment, e.g. p // The first person passed through without payingl: C,C,P,P,P,C,P // The first person paid for the one behind them, but two people behind them passed throught Design a PDA over the input alphabet ={C,P} that accepts input strings which reflect proper turnstile operation, and reject other inputs. You may use any stack alphabet, F. ( F is the set of symbols that can be pushed onto the stack. It typically contains some or all of the symbols from the alphabet, 2 , plus some others.) Design a PDA over the input alphabet ={C,P} that accepts input strings which reflect proper turnstile operation, and reject other inputs. You may use any stack alphabet, . ( is the set of symbols that can be pushed onto the stack. It typically contains some or all of the symbols from the alphabet, , plus some others.) There is a solution that can be obtained by labeling the arrows in this diagram: 2. (20 points) Consider a turnstile like we did in the first lecture of the course. Assume it is coin operated, and an intern at the company that makes it is given the following task: Sit in a subway station where these machines are in use. Wotch one of them all day, from its initial power-on at 5 am until powerdown at midnight. Write down a symbol for each of the following observed events in the order they occur: C for: "coin goes in", and "p" for "person passes through". Proper turnstile operation: - The power-on state is tocked. - Dropping in a coin stores the coin and puts the turnstile in the unlocked state. - A person cannot Pass when the turnstile is locked. - Passing through the turnstile moves it to the locked state, and consumes a stored coin. - The turnstile allows a person to drop in as many coins as they want, and these will each be stored and used to pay for subsequent subway passengers. - At the end of the day, there may be unused coins stored in the turnstile. Observing a properly working turnstile, the intern might record, e.g. C,P,C,C,P,P // The second person paid for the one behind them/ C,C,C,C,P // The first person for 3 more people, but none showed A faulty turnstile would allow someone through without payment, e.g. p // The first person passed through without payingl: C,C,P,P,P,C,P // The first person paid for the one behind them, but two people behind them passed throught Design a PDA over the input alphabet ={C,P} that accepts input strings which reflect proper turnstile operation, and reject other inputs. You may use any stack alphabet, F. ( F is the set of symbols that can be pushed onto the stack. It typically contains some or all of the symbols from the alphabet, 2 , plus some others.) Design a PDA over the input alphabet ={C,P} that accepts input strings which reflect proper turnstile operation, and reject other inputs. You may use any stack alphabet, . ( is the set of symbols that can be pushed onto the stack. It typically contains some or all of the symbols from the alphabet, , plus some others.) There is a solution that can be obtained by labeling the arrows in this diagram