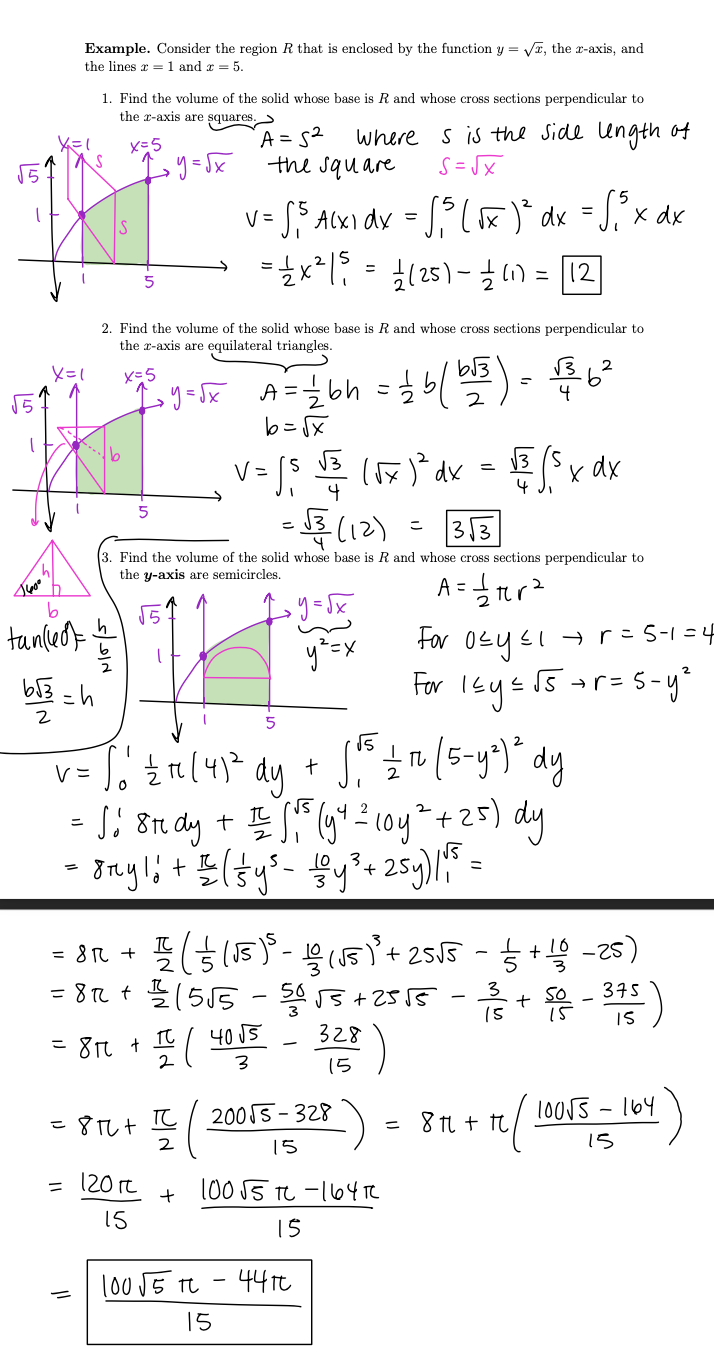
2. (3 points each) Consider the region R bounded by the x-axis, the y-axis, y = 4, and y= (x-3). (a) Sketch a graph of the region. (You should attempt this problem on your own first, but you may use Desmos to verify your answer.) (b) Write, but do not evaluate, an integral in terms of x which gives the area of the region R. (c) Write, but do not evaluate, an integral in terms of y which gives the area of the region R. (d) Write, but do not evaluate, an integral which gives the volume of the solid whose base is R and whose cross-sections perpendicular to the x-axis are squares. (e) Write, but do not evaluate, an integral which gives the volume of the solid whose base is R and whose cross-sections perpendicular to the z-axis are semi-circles. (f) Write, but do not evaluate, an integral which gives the volume of the solid whose base is R and whose cross-sections perpendicular to the y-axis are squares. (g) Write, but do not evaluate, an integral which gives the volume of the solid formed by rotating R around the z-axis. (h) Write, but do not evaluate, an integral which gives the volume of the solid formed by rotating R around the y-axis. 1. Express and compute the volume of a solid in terms of a definite integral of its cross- sectional areas. 2. Compute the volumes of solids of revolution about the x- or y-axis by using the disk method or washer method. Suppose we want to compute the volume of the solid shown below. We can approximate the volume by splitting the solid into n "slabs" S1, S2, ... Sn each of thickness Ax. Define A(x) to be... a=X x x 33 x=b Area = A(x*) the area of a cross-section of the solid at a given x-value If we choose a special point x in each slab Si, then the volume of S; is approximately... A(x)4x Therefore, the volume of the solid is approximately... A(xi) AX i=1 We can compute the EXACT volume using. lim A(xi) ax b = So A ( x ) d x a 1 Concussion: Find volume by integrating the Cross-sectional area over [a,b]. X=1 Example. Consider the region R that is enclosed by the function y = x, the x-axis, and the lines 1 and x = 5. 1. Find the volume of the solid whose base is R and whose cross sections perpendicular to the x-axis are squares. x=5 A = 52 Where s is the side length of - y = x the square S=x v = ,5 Alx1 dx = ,5 (x) * dx = ,"x dx =x215 = {(25)-()= 12 2. Find the volume of the solid whose base is R and whose cross sections perpendicular to the x-axis are equilateral triangles. X=1 x=5 5 5 A = 1/16h = 1 b (b13 ) = 1362 b=x 2 4 v = s 3 (1x) dx = 5 x dx V =3(12) 4 = 33 3. Find the volume of the solid whose base is R and whose cross sections perpendicular to the y-axis are semicircles. J600 b tanko 653-h 2 For 0ysi 1 r = 5-1 =4 For 1 y 5 + r = 5-y 5 5 v = S = (4) dy + 11 (5-y) dy T' 2 2 = 1; 8 dy + 12 (1 (y = loy +25) dy - 8y!! + = ( y - 10 y + 25y) 11.5 = = = 8 + 2 = (1/3 10 (15) ( (15) - (55) + 255 - 1/3 + 1060 - 25) = 8 + 1/2 155 - 50 3 +2515 - 336 + 50 - 3+5) = 8 + 11 ( 4015 - 328 ) 2 3 15 - 164 = 8 + C 20055-328 = 8 + 10055 2 15 15 = 120 + 1005 -1647 = 15 1005 15 4410 15