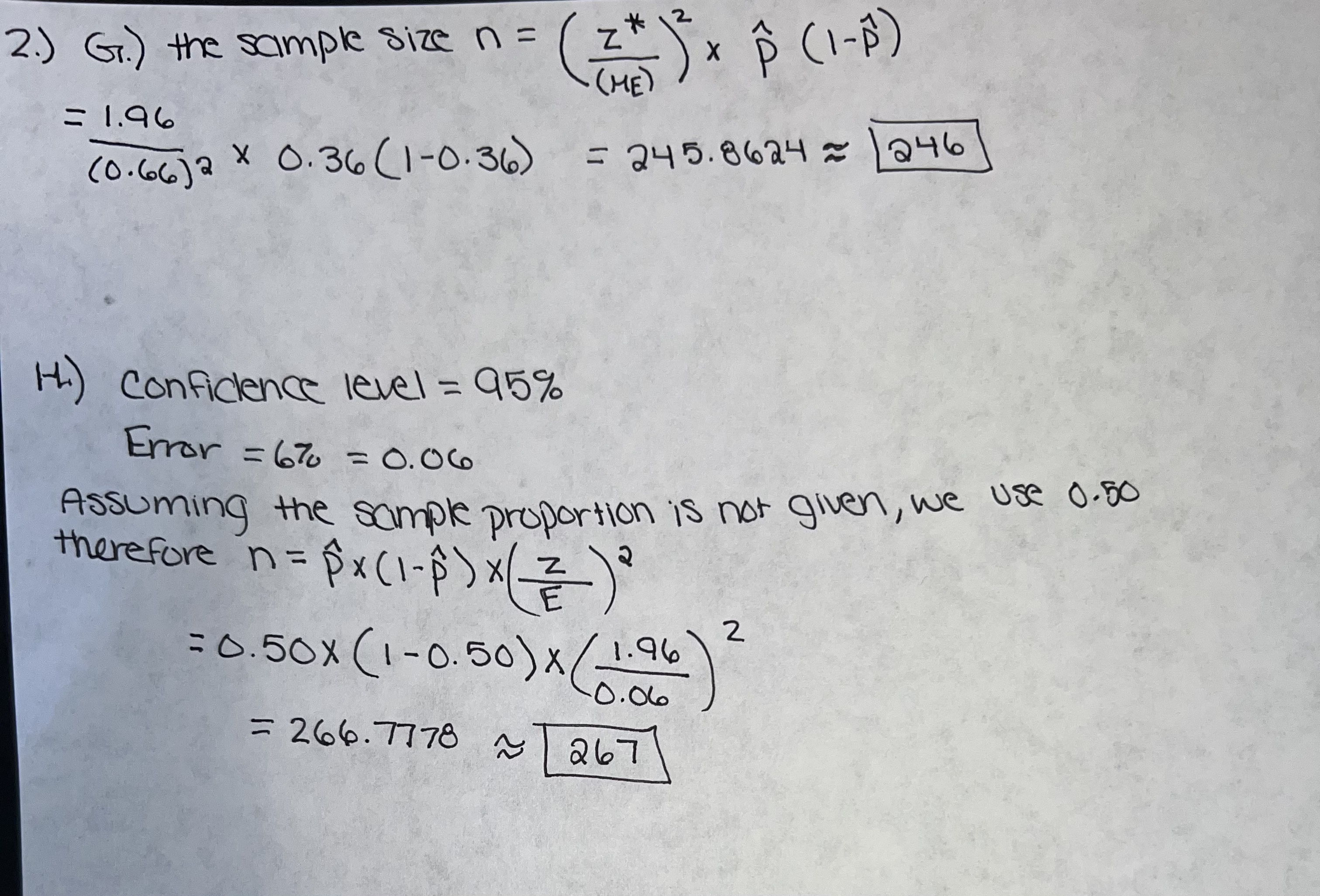
2. A nurse in a large university (N = 30,000) is concerned about students' eye health. She takes a random sample of 75 students who don't wear glasses and finds 27 that need glasses. What's the point estimate of p, the population proportion? (1 point) B. Is the situation binomial? Also, can the z-distribution be used to calculate a confidence interval for the proportion of students who need glasses but don't wear them? Explain. (2 points) What's the critical z-value (z*) for a 90% confidence interval for the population proportion? (1 point) What's the margin of error for a 90% confidence interval for the population proportion? (2 points) E. Calculate the 90% confidence interval for the population proportion. (1 point) Using your graphing calculator, find a 95% confidence interval for the proportion of students who need to wear glasses but don't. (Show all work, functions, and inputs on your calculator too. (1 point) The nurse wants to be able to estimate, with a 95% confidence interval and a margin of error of 6%, the proportion of students who need to wear glasses but don't. Find the necessary sample size (n) for this estimate. (2 points) H. The following school year, the nurse wants to construct the same 95% confidence interval for the proportion of students who need glasses but don't wear them, but she thinks the proportion has changed since last year. Without using the point estimate of the population proportion from the previous year, find the necessary sample size (n) for a 95% confidence interval for the population proportion with a margin of error (m) of 6%. (2 points) Z 2 2.) G.) the sample size n = (z+1) x (1-8) = 1.96 (ME) (0.66) 2 x 0.36 (1-0.36) = 245.8624 1246 H.) Confidence level = 95% Error = 6% = 0.06 therefore n = 1x (1 - p) x ( ) Assuming the sample proportion is not given, we use 0.80 = 0.50x (1-0.50) x (1.96 = 266.7778 ~ 0.06 ~ [267 2 2.) a.) P = x/n = 27/75 =0.36 P=x/n b.) Yes, the situation is binomial because each student either needs glasses or doesn't. Therefore the z-distribution can be used to calculate a confidence interval for the proportion of Stuckents who need glasses but won't wear them because the sample size is Sufficiently large (n = 75>30) and the population proportion is unknown. C.) The critical z-value (z*) for a 90% confidence interval for the Population proportion is 1.645 d.) The Margin of Error for a 90% confidence interval X ME = Z* P(1-P) 1.645x 0.36 (1-0.36) 75 = 0.09117515451 ME = 10.0912 e.) The 90% Confidence interval for the population proportion can be Calculated as: = ME = (0.36+0.0912) = 10.4512 $-ME = (0.36 -0.0912) = 10.2688 range is = (0.2688, 0.4512) F.) 95% confidence level has z-score of 1.96 1.96x 0.36 (1-0.36) 75 ME = 0.1086 Confidence Interval = 0.360.1086 (0.2514, 0.4686