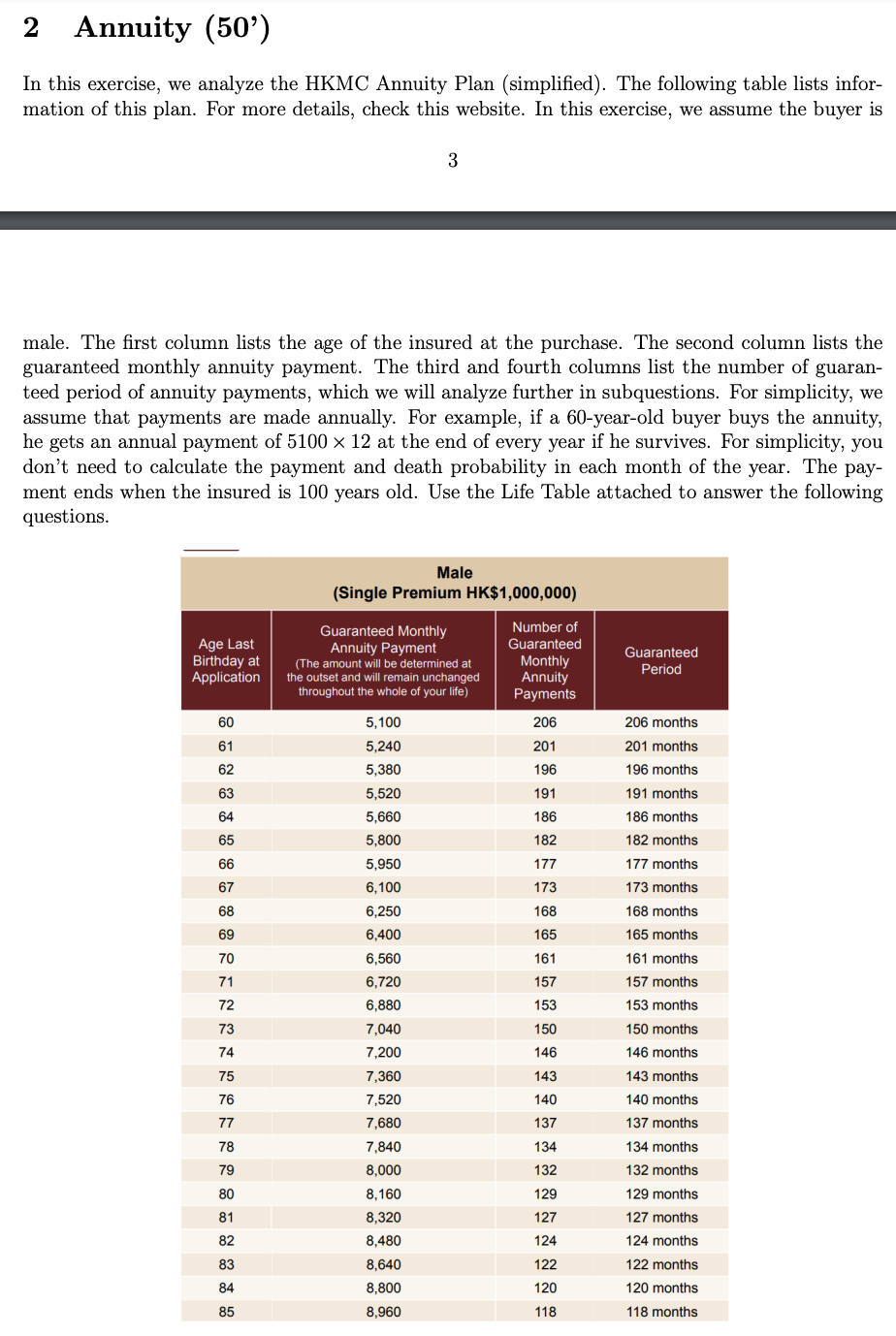

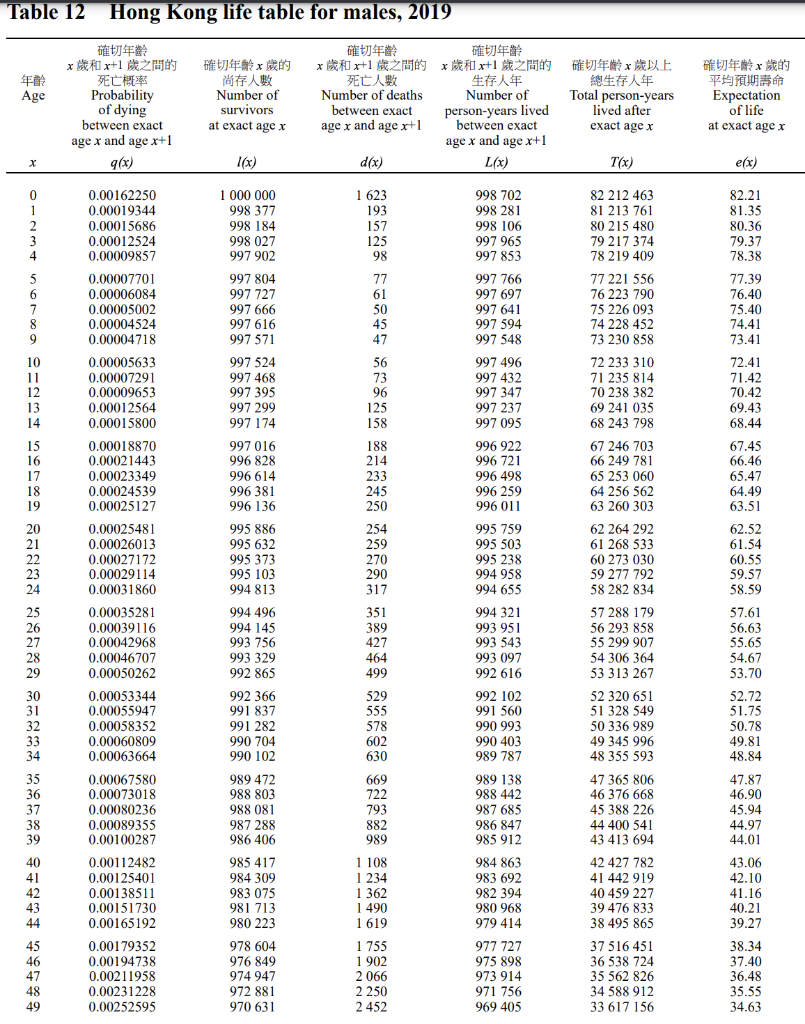
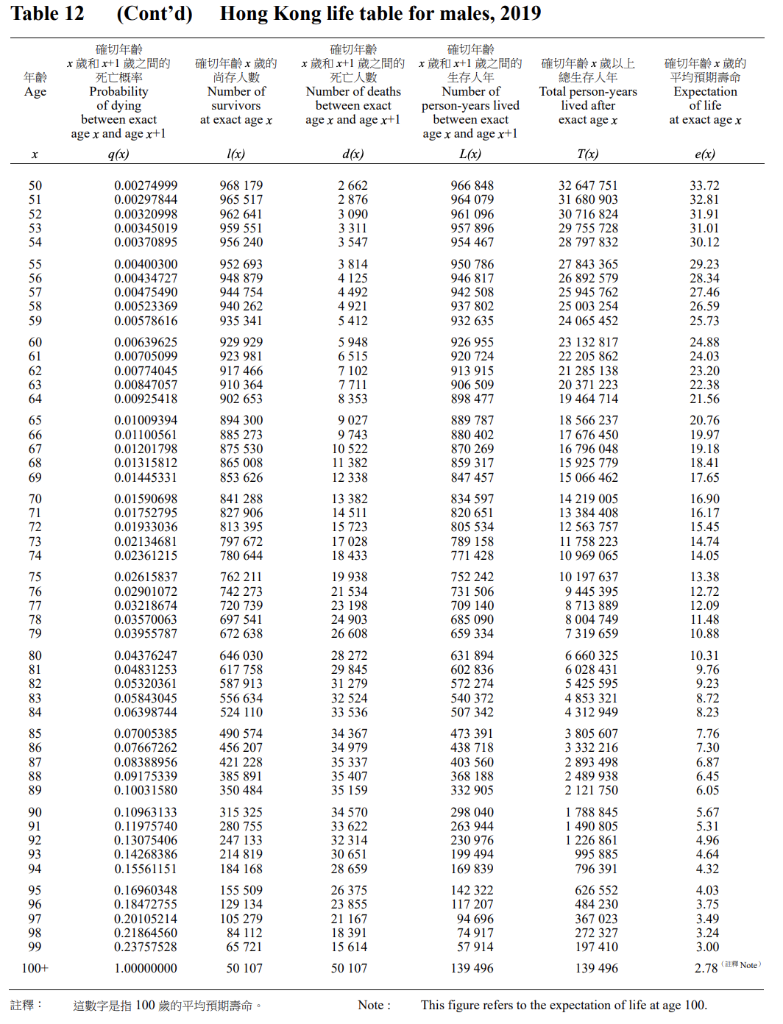
2 Annuity (50) In this exercise, we analyze the HKMC Annuity Plan (simplified). The following table lists infor- mation of this plan. For more details, check this website. In this exercise, we assume the buyer is 3 male. The first column lists the age of the insured at the purchase. The second column lists the guaranteed monthly annuity payment. The third and fourth columns list the number of guaran- teed period of annuity payments, which we will analyze further in subquestions. For simplicity, we assume that payments are made annually. For example, if a 60-year-old buyer buys the annuity, he gets an annual payment of 5100 x 12 at the end of every year if he survives. For simplicity, you don't need to calculate the payment and death probability in each month of the year. The pay- ment ends when the insured is 100 years old. Use the Life Table attached to answer the following questions. Male (Single Premium HK$1,000,000) Age Last Birthday at Application Guaranteed Monthly Annuity Payment (The amount will be determined at the outset and will remain unchanged throughout the whole of your life) Guaranteed Period 60 61 Number of Guaranteed Monthly Annuity Payments 206 201 196 191 186 62 206 months 201 months 196 months 191 months 186 months 182 months 63 64 65 182 66 177 5,100 5,240 5,380 5,520 5,660 5,800 5,950 6,100 6,250 6,400 6,560 6,720 6,880 7,040 7,200 67 68 173 168 177 months 173 months 168 months 165 months 161 months 157 months 69 165 70 71 72 161 157 153 153 months 150 73 74 150 months 146 months 146 75 143 143 months 76 140 140 months 77 137 134 78 79 80 7,360 7,520 7,680 7,840 8,000 8,160 8,320 8,480 8,640 8,800 8,960 132 129 127 124 81 82 137 months 134 months 132 months 129 months 127 months 124 months 122 months 120 months 118 months 83 122 84 120 85 118 1. Suppose the policy does not have any death benefit, which means if the insured dies the policy stops making payments. Assume the policyholder does not surrender the policy before death. (15') (a) Calculate the internal rate of return (IRR) of this policy for buyers of 60 (the buyer is right before his 60th birthday). Assume the first payment starts one year later. (10') 4 (b) Suppose there is another financial instrument (e.g., a bond) that can achieve the same level of IRR as you calculate in part (a). What is the benefit of the annuity plan, compared with the alternative instrument? (5') Table 12 Hong Kong life table for males, 2019 Age rx+1 Probability of dying between exact age x and age x+1 q(x) x Number of survivors at exact age x x +1 x+1 Number of deaths Number of between exact person-years lived age x and age x+1 between exact age x and age x+1 d) d(x) L(x) r Total person-years lived after exact age x x Expectation of life at exact ager x (x) T(x) Tics (x) 1 623 193 157 125 98 77 61 50 45 47 0.00162250 0.00019344 0.00015686 0.00012524 0.00009857 0.00007701 0.00006084 0.00005002 0.00004524 0.00004718 0.00005633 0.00007291 0.00009653 0.00012564 0.00015800 0.00018870 0.00021443 0.00023349 0.00024539 0.00025127 0.00025481 0.00026013 0.00027172 0.00029114 0.00031860 1 000 000 998 377 998 184 998 027 997 902 997 804 997 727 997 666 997 616 997 571 997 524 997 468 997 395 997 299 997 174 997 016 996 828 996 614 996 381 996 136 10 11 12 13 14 82.21 81.35 80.36 79.37 78.38 77.39 76.40 75.40 74.41 73.41 72.41 71.42 70.42 69.43 68.44 67.45 66.46 56 73 96 125 158 998 702 998 281 998 106 997 965 997 853 997 766 997 697 997 641 997 594 997 548 997 496 997 432 997 347 997 237 997 095 996 922 996 721 996 498 996 259 996 011 995 759 995 503 995 238 994 958 994 655 994 321 993 951 993 543 993 097 992 616 15 16 17 18 19 188 214 233 245 250 65.47 64.49 63.51 01234 56789 WHQSH BETWD943u8%a8ww=%B4% 20 21 22 23 24 25 26 27 28 29 254 259 270 290 317 351 389 427 464 499 82 212 463 81 213 761 80 215 480 79 217 374 78 219 409 77 221 556 76 223 790 75 226 093 74 228 452 73 230 858 72 233 310 71 235 814 70 238 382 69 241 035 68 243 798 67 246 703 66 249 781 65 253 060 64 256 562 63 260 303 62 264 292 61 268 533 60 273 030 59 277 792 58 282 834 57 288 179 56 293 858 55 299 907 54 306 364 53 313 267 52 320 651 51 328 549 50 336 989 49 345 996 48 355 593 47 365 806 46 376 668 45 388 226 44 400 541 43 413 694 42 427 782 41 442 919 40 459 227 39 476 833 38 495 865 37 516 451 36 538 724 35 562 826 34 588 912 33 617 156 62.52 61.54 60.55 59.57 58.59 57.61 56.63 55.65 54.67 53.70 529 555 578 602 630 52.72 51.75 50.78 49.81 48.84 30 31 32 33 34 35 36 37 38 39 995 886 995 632 995 373 995 103 994 813 994 496 994 145 993 756 993 329 992 865 992 366 991 837 991 282 990 704 990 102 989 472 988 803 988 081 987 288 986 406 985 417 984 309 983 075 981 713 980 223 978 604 976 849 974 947 972 881 970 631 0.00035281 0.00039116 0.00042968 0.00046707 0.00050262 0.00053344 0.00055947 0.00058352 0.00060809 0.00063664 0.00067580 0.00073018 0.00080236 0.00089355 0.00100287 0.00112482 0.00125401 0.00138511 0.00151730 0.00165192 0.00179352 0.00194738 0.00211958 0.00231228 0.00252595 669 722 793 882 989 47.87 46.90 45.94 44.97 44.01 992 102 991 560 990 993 990 403 989 787 989 138 988 442 987 685 986 847 985 912 984 863 983 692 982 394 980 968 979 414 977 727 975 898 973 914 971 756 969 405 40 41 42 43 44 43.06 42.10 41.16 40.21 39.27 1 108 1 1 234 1 362 1 490 1619 1 755 1 902 2 066 2 250 2 452 45 46 47 48 49 38.34 37.40 36.48 35.55 34.63 Table 12 (Cont'd) Hong Kong life table for males, 2019 x x+1 Probability Age x Number of survivors at exact ager +1x+1 Number of deaths Number of between exact person-years lived age x and age x+1 between exact age x and age x+1 dx) d(x) L(x) Total person-years lived after exact age x Expectation of life at exact age x of dying between exact age x and age x+1 96x) In ) Tax) efx) e(x) 50 51 52 53 54 33.72 32.81 31.91 31.01 30.12 55 56 57 58 59 968 179 965 517 962 641 959 551 956 240 952 693 948 879 944 754 940 262 935 341 929 929 923 981 917 466 2662 2 876 3 090 3311 3 547 3 814 4 4 125 4 4 492 4921 5412 5948 6 515 7 102 7 29.23 28.34 27.46 26.59 25.73 24.88 24.03 23.20 22.38 21.56 60 61 62 910 364 7711 63 64 902 653 8 353 65 66 67 68 69 70 71 72 73 74 r%3B8% 5%%w mdas SSGgs 229 www8w %%%%%%%%%%%% w 0.00274999 0.00297844 0.00320998 0.00345019 0.00370895 0.00400300 0.00434727 0.00475490 0.00523369 0.00578616 0.00639625 0.00705099 0.00774045 0.00847057 0.00925418 0.01009394 0.01100561 0.01201798 0.01315812 0.01445331 0.01590698 0.01752795 0.01933036 0.02134681 0.02361215 0.02615837 0.02901072 0.03218674 0.03570063 0.03955787 0.04376247 0.04831253 0.05320361 0.05843045 0.06398744 0.07005385 0.07667262 0.08388956 0.09175339 0.10031580 0.10963133 0.11975740 0.13075406 0.14268386 0.15561151 0.16960348 0.18472755 0.20105214 0.21864560 0.23757528 1.00000000 894 300 885 273 875 530 865 008 853 626 841 288 827 906 813 395 797 672 780 644 762 211 742 273 720 739 697 541 672 638 9027 9 743 10 522 11 382 12 338 13 382 14 511 15 723 17 028 18 433 19 938 21 534 23 198 24 903 26 608 966 848 964 079 961 096 957 896 954 467 950 786 946 817 942 508 937 802 932 635 926 955 920 724 913 915 906 509 898 477 889 787 880 402 870 269 859 317 847 457 834 597 820 651 805 534 789 158 771 428 752 242 731 506 709 140 685 090 659 334 631 894 602 836 572 274 540 372 507 342 473 391 438 718 403 560 368 188 332 905 298 040 263 944 230 976 32 647 751 31 680 903 30 716 824 29 755 728 28 797 832 27 843 365 26 892 579 25 945 762 25 003 254 24 065 452 23 132 817 22 205 862 21 285 138 20 371 223 19 464 714 18 566 237 17 676 450 16 796 048 15 925 779 15 066 462 14 219 005 13 384 408 12 563 757 11 758 223 10 969 065 10 197 637 9 445 395 8 713 889 8 004 749 7319 659 6 660 325 6028 431 5425 595 4 853 321 4 312 949 3 805 607 3 332 216 2 893 498 2 2 489 938 2 121 750 1 788 845 1 490 805 1 226 861 995 885 796 391 626 552 484 230 367 023 272 327 197 410 75 76 77 78 79 20.76 19.97 19.18 18.41 17.65 16.90 16.17 15.45 14.74 14.05 13.38 12.72 12.09 11.48 10.88 10.31 9.76 9.23 8.72 8.23 7.76 7.30 6.87 6.45 6.05 80 81 82 83 84 646 030 617 758 587 913 556 634 524 110 490 574 456 207 85 86 87 88 89 421 228 385 891 350 484 315 325 280 755 247 133 90 91 92 93 94 28 272 29 845 31 279 32 524 33 536 34 367 34 979 35 337 35 407 35 159 34 570 33 622 32 314 30 651 28 659 26 375 23 855 21 167 18 391 15 614 50 107 5.67 5.31 4.96 4.64 4.32 214 819 199 494 95 96 97 98 99 184 168 155 509 129 134 105 279 84 112 65 721 50 107 169 839 142 322 117 207 94 696 74 917 57 914 139 496 4.03 3.75 3.49 3.24 3.00 100+ 139 496 2.78 Muse : 100 Note: This figure refers to the expectation of life at age 100. 2 Annuity (50) In this exercise, we analyze the HKMC Annuity Plan (simplified). The following table lists infor- mation of this plan. For more details, check this website. In this exercise, we assume the buyer is 3 male. The first column lists the age of the insured at the purchase. The second column lists the guaranteed monthly annuity payment. The third and fourth columns list the number of guaran- teed period of annuity payments, which we will analyze further in subquestions. For simplicity, we assume that payments are made annually. For example, if a 60-year-old buyer buys the annuity, he gets an annual payment of 5100 x 12 at the end of every year if he survives. For simplicity, you don't need to calculate the payment and death probability in each month of the year. The pay- ment ends when the insured is 100 years old. Use the Life Table attached to answer the following questions. Male (Single Premium HK$1,000,000) Age Last Birthday at Application Guaranteed Monthly Annuity Payment (The amount will be determined at the outset and will remain unchanged throughout the whole of your life) Guaranteed Period 60 61 Number of Guaranteed Monthly Annuity Payments 206 201 196 191 186 62 206 months 201 months 196 months 191 months 186 months 182 months 63 64 65 182 66 177 5,100 5,240 5,380 5,520 5,660 5,800 5,950 6,100 6,250 6,400 6,560 6,720 6,880 7,040 7,200 67 68 173 168 177 months 173 months 168 months 165 months 161 months 157 months 69 165 70 71 72 161 157 153 153 months 150 73 74 150 months 146 months 146 75 143 143 months 76 140 140 months 77 137 134 78 79 80 7,360 7,520 7,680 7,840 8,000 8,160 8,320 8,480 8,640 8,800 8,960 132 129 127 124 81 82 137 months 134 months 132 months 129 months 127 months 124 months 122 months 120 months 118 months 83 122 84 120 85 118 1. Suppose the policy does not have any death benefit, which means if the insured dies the policy stops making payments. Assume the policyholder does not surrender the policy before death. (15') (a) Calculate the internal rate of return (IRR) of this policy for buyers of 60 (the buyer is right before his 60th birthday). Assume the first payment starts one year later. (10') 4 (b) Suppose there is another financial instrument (e.g., a bond) that can achieve the same level of IRR as you calculate in part (a). What is the benefit of the annuity plan, compared with the alternative instrument? (5') Table 12 Hong Kong life table for males, 2019 Age rx+1 Probability of dying between exact age x and age x+1 q(x) x Number of survivors at exact age x x +1 x+1 Number of deaths Number of between exact person-years lived age x and age x+1 between exact age x and age x+1 d) d(x) L(x) r Total person-years lived after exact age x x Expectation of life at exact ager x (x) T(x) Tics (x) 1 623 193 157 125 98 77 61 50 45 47 0.00162250 0.00019344 0.00015686 0.00012524 0.00009857 0.00007701 0.00006084 0.00005002 0.00004524 0.00004718 0.00005633 0.00007291 0.00009653 0.00012564 0.00015800 0.00018870 0.00021443 0.00023349 0.00024539 0.00025127 0.00025481 0.00026013 0.00027172 0.00029114 0.00031860 1 000 000 998 377 998 184 998 027 997 902 997 804 997 727 997 666 997 616 997 571 997 524 997 468 997 395 997 299 997 174 997 016 996 828 996 614 996 381 996 136 10 11 12 13 14 82.21 81.35 80.36 79.37 78.38 77.39 76.40 75.40 74.41 73.41 72.41 71.42 70.42 69.43 68.44 67.45 66.46 56 73 96 125 158 998 702 998 281 998 106 997 965 997 853 997 766 997 697 997 641 997 594 997 548 997 496 997 432 997 347 997 237 997 095 996 922 996 721 996 498 996 259 996 011 995 759 995 503 995 238 994 958 994 655 994 321 993 951 993 543 993 097 992 616 15 16 17 18 19 188 214 233 245 250 65.47 64.49 63.51 01234 56789 WHQSH BETWD943u8%a8ww=%B4% 20 21 22 23 24 25 26 27 28 29 254 259 270 290 317 351 389 427 464 499 82 212 463 81 213 761 80 215 480 79 217 374 78 219 409 77 221 556 76 223 790 75 226 093 74 228 452 73 230 858 72 233 310 71 235 814 70 238 382 69 241 035 68 243 798 67 246 703 66 249 781 65 253 060 64 256 562 63 260 303 62 264 292 61 268 533 60 273 030 59 277 792 58 282 834 57 288 179 56 293 858 55 299 907 54 306 364 53 313 267 52 320 651 51 328 549 50 336 989 49 345 996 48 355 593 47 365 806 46 376 668 45 388 226 44 400 541 43 413 694 42 427 782 41 442 919 40 459 227 39 476 833 38 495 865 37 516 451 36 538 724 35 562 826 34 588 912 33 617 156 62.52 61.54 60.55 59.57 58.59 57.61 56.63 55.65 54.67 53.70 529 555 578 602 630 52.72 51.75 50.78 49.81 48.84 30 31 32 33 34 35 36 37 38 39 995 886 995 632 995 373 995 103 994 813 994 496 994 145 993 756 993 329 992 865 992 366 991 837 991 282 990 704 990 102 989 472 988 803 988 081 987 288 986 406 985 417 984 309 983 075 981 713 980 223 978 604 976 849 974 947 972 881 970 631 0.00035281 0.00039116 0.00042968 0.00046707 0.00050262 0.00053344 0.00055947 0.00058352 0.00060809 0.00063664 0.00067580 0.00073018 0.00080236 0.00089355 0.00100287 0.00112482 0.00125401 0.00138511 0.00151730 0.00165192 0.00179352 0.00194738 0.00211958 0.00231228 0.00252595 669 722 793 882 989 47.87 46.90 45.94 44.97 44.01 992 102 991 560 990 993 990 403 989 787 989 138 988 442 987 685 986 847 985 912 984 863 983 692 982 394 980 968 979 414 977 727 975 898 973 914 971 756 969 405 40 41 42 43 44 43.06 42.10 41.16 40.21 39.27 1 108 1 1 234 1 362 1 490 1619 1 755 1 902 2 066 2 250 2 452 45 46 47 48 49 38.34 37.40 36.48 35.55 34.63 Table 12 (Cont'd) Hong Kong life table for males, 2019 x x+1 Probability Age x Number of survivors at exact ager +1x+1 Number of deaths Number of between exact person-years lived age x and age x+1 between exact age x and age x+1 dx) d(x) L(x) Total person-years lived after exact age x Expectation of life at exact age x of dying between exact age x and age x+1 96x) In ) Tax) efx) e(x) 50 51 52 53 54 33.72 32.81 31.91 31.01 30.12 55 56 57 58 59 968 179 965 517 962 641 959 551 956 240 952 693 948 879 944 754 940 262 935 341 929 929 923 981 917 466 2662 2 876 3 090 3311 3 547 3 814 4 4 125 4 4 492 4921 5412 5948 6 515 7 102 7 29.23 28.34 27.46 26.59 25.73 24.88 24.03 23.20 22.38 21.56 60 61 62 910 364 7711 63 64 902 653 8 353 65 66 67 68 69 70 71 72 73 74 r%3B8% 5%%w mdas SSGgs 229 www8w %%%%%%%%%%%% w 0.00274999 0.00297844 0.00320998 0.00345019 0.00370895 0.00400300 0.00434727 0.00475490 0.00523369 0.00578616 0.00639625 0.00705099 0.00774045 0.00847057 0.00925418 0.01009394 0.01100561 0.01201798 0.01315812 0.01445331 0.01590698 0.01752795 0.01933036 0.02134681 0.02361215 0.02615837 0.02901072 0.03218674 0.03570063 0.03955787 0.04376247 0.04831253 0.05320361 0.05843045 0.06398744 0.07005385 0.07667262 0.08388956 0.09175339 0.10031580 0.10963133 0.11975740 0.13075406 0.14268386 0.15561151 0.16960348 0.18472755 0.20105214 0.21864560 0.23757528 1.00000000 894 300 885 273 875 530 865 008 853 626 841 288 827 906 813 395 797 672 780 644 762 211 742 273 720 739 697 541 672 638 9027 9 743 10 522 11 382 12 338 13 382 14 511 15 723 17 028 18 433 19 938 21 534 23 198 24 903 26 608 966 848 964 079 961 096 957 896 954 467 950 786 946 817 942 508 937 802 932 635 926 955 920 724 913 915 906 509 898 477 889 787 880 402 870 269 859 317 847 457 834 597 820 651 805 534 789 158 771 428 752 242 731 506 709 140 685 090 659 334 631 894 602 836 572 274 540 372 507 342 473 391 438 718 403 560 368 188 332 905 298 040 263 944 230 976 32 647 751 31 680 903 30 716 824 29 755 728 28 797 832 27 843 365 26 892 579 25 945 762 25 003 254 24 065 452 23 132 817 22 205 862 21 285 138 20 371 223 19 464 714 18 566 237 17 676 450 16 796 048 15 925 779 15 066 462 14 219 005 13 384 408 12 563 757 11 758 223 10 969 065 10 197 637 9 445 395 8 713 889 8 004 749 7319 659 6 660 325 6028 431 5425 595 4 853 321 4 312 949 3 805 607 3 332 216 2 893 498 2 2 489 938 2 121 750 1 788 845 1 490 805 1 226 861 995 885 796 391 626 552 484 230 367 023 272 327 197 410 75 76 77 78 79 20.76 19.97 19.18 18.41 17.65 16.90 16.17 15.45 14.74 14.05 13.38 12.72 12.09 11.48 10.88 10.31 9.76 9.23 8.72 8.23 7.76 7.30 6.87 6.45 6.05 80 81 82 83 84 646 030 617 758 587 913 556 634 524 110 490 574 456 207 85 86 87 88 89 421 228 385 891 350 484 315 325 280 755 247 133 90 91 92 93 94 28 272 29 845 31 279 32 524 33 536 34 367 34 979 35 337 35 407 35 159 34 570 33 622 32 314 30 651 28 659 26 375 23 855 21 167 18 391 15 614 50 107 5.67 5.31 4.96 4.64 4.32 214 819 199 494 95 96 97 98 99 184 168 155 509 129 134 105 279 84 112 65 721 50 107 169 839 142 322 117 207 94 696 74 917 57 914 139 496 4.03 3.75 3.49 3.24 3.00 100+ 139 496 2.78 Muse : 100 Note: This figure refers to the expectation of life at age 100










