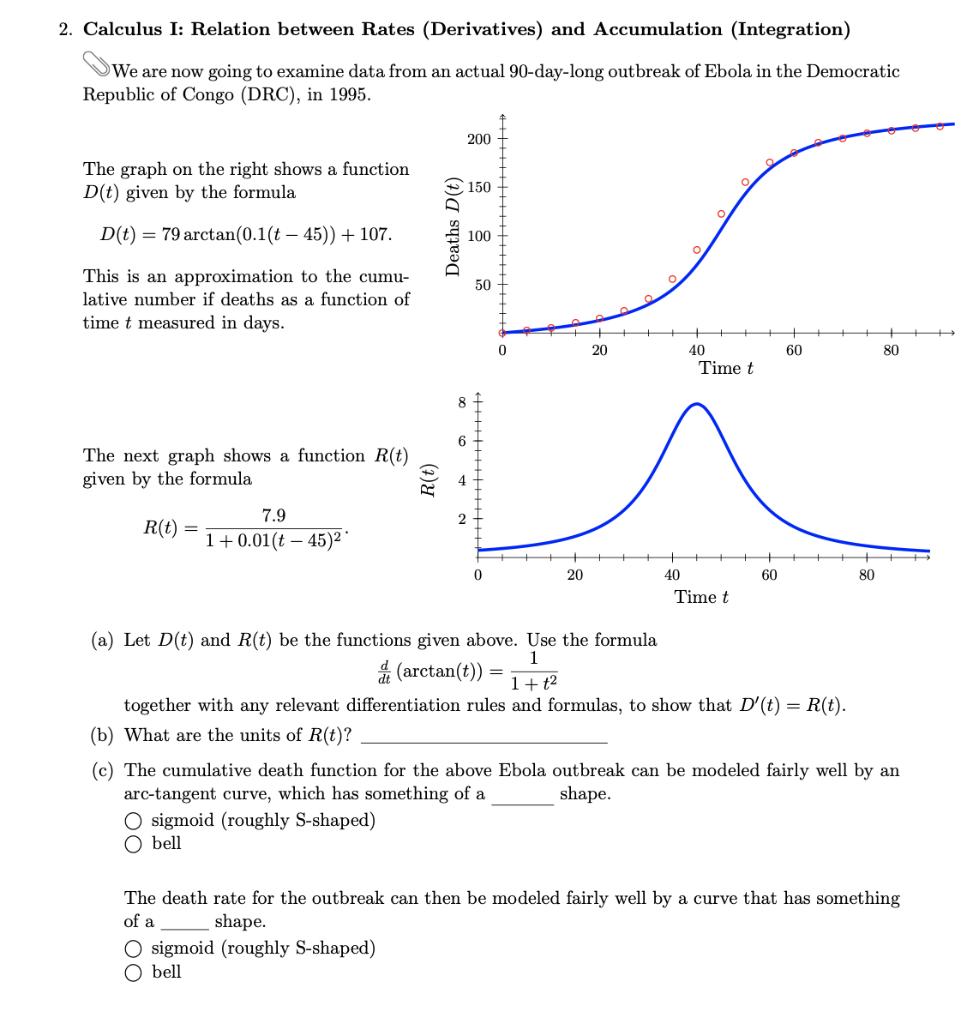
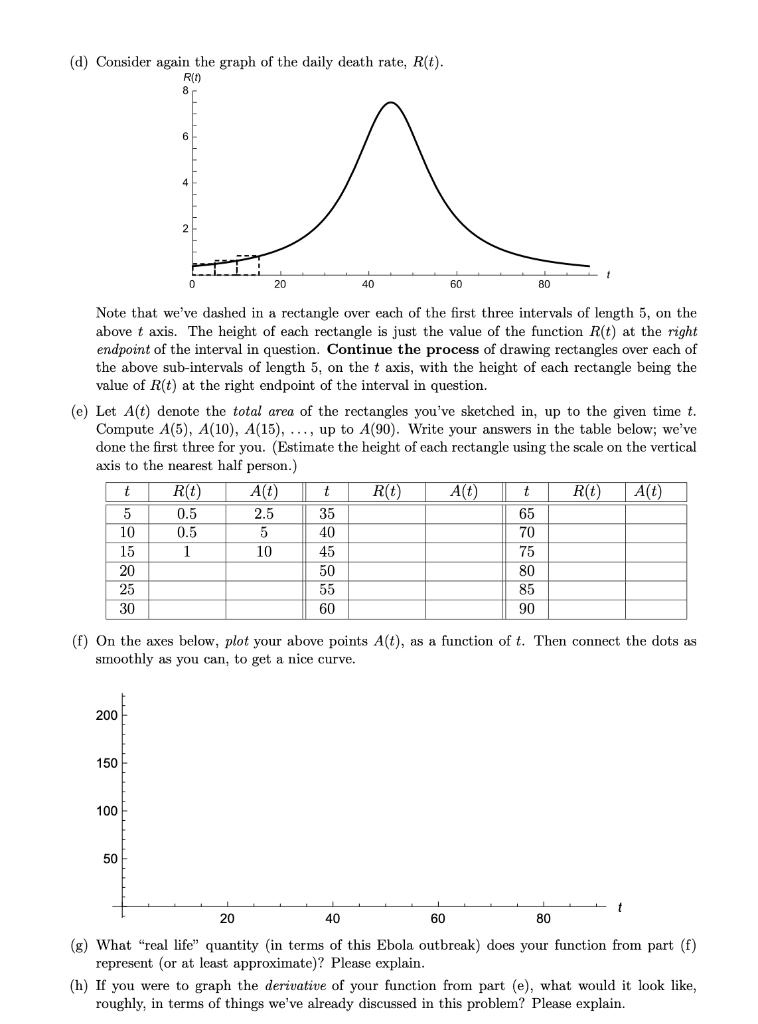
2. Calculus I: Relation between Rates (Derivatives) and Accumulation (Integration) We are now going to examine data from an actual 90-day-long outbreak of Ebola in the Democratic Republic of Congo (DRC), in 1995. The graph on the right shows a function D(t) given by the formula D(t) 79 arctan(0.1(t-45)) + 107. This is an approximation to the cumu- lative number if deaths as a function of time t measured in days. The next graph shows a function R(t) given by the formula R(t) 8 200 Deaths D(t) 50 50 100 150 +1 0 20 40 60 80 Time t 7.9 R(t) = 1+0.01 (t - 45) 0 20 40 60 80 Time t (a) Let D(t) and R(t) be the functions given above. Use the formula (arctan(t)) = 1 1+t2 together with any relevant differentiation rules and formulas, to show that D'(t) = R(t). (b) What are the units of R(t)? (c) The cumulative death function for the above Ebola outbreak can be modeled fairly well by an arc-tangent curve, which has something of a O sigmoid (roughly S-shaped) O bell shape. The death rate for the outbreak can then be modeled fairly well by a curve that has something of a shape. O sigmoid (roughly S-shaped) O bell (d) Consider again the graph of the daily death rate, R(t).. R(t) 8 6 4 2 20 40 60 80 Note that we've dashed in a rectangle over each of the first three intervals of length 5, on the above t axis. The height of each rectangle is just the value of the function R(t) at the right endpoint of the interval in question. Continue the process of drawing rectangles over each of the above sub-intervals of length 5, on the t axis, with the height of each rectangle being the value of R(t) at the right endpoint of the interval in question. (e) Let A(t) denote the total area of the rectangles you've sketched in, up to the given time t. Compute A(5), A(10), A(15), ..., up to A(90). Write your answers in the table below; we've done the first three for you. (Estimate the height of each rectangle using the scale on the vertical axis to the nearest half person.) t R(t) A(t) t R(t) A(t) t R(t) A(t) 5 0.5 2.5 35 65 10 0.5 5 40 70 15 1 10 45 75 20 50 80 25 55 85 30 60 90 (f) On the axes below, plot your above points A(t), as a function of t. Then connect the dots as smoothly as you can, to get a nice curve. 200 150 100 50 20 40 60 80 (g) What "real life" quantity (in terms of this Ebola outbreak) does your function from part (f) represent (or at least approximate)? Please explain. (h) If you were to graph the derivative of your function from part (e), what would it look like, roughly, in terms of things we've already discussed in this problem? Please explain.