2. Compute the optimal policy for the decision network by using the variable elimination algorithm. Assume that p1 = 1/3 and p2 = 1/3. Show all your work including all the intermediate factors created. Clearly indicate the optimal policy and the expected utility of the agent following the optimal policy.

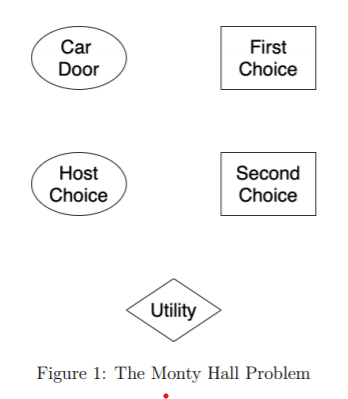
The Monty Hall Problem is stated as follows. You are on a game show, and you are given the choice of three doors: Behind one door is a car; behind the others, goats. The host knows what's behind each door but you don't. First, you pick a door, say Door 1. Second, the host opens another door, say Door 3, which has a goat behind it. Finally, the host says to you, Do you want to pick Door 2?" Is it to your advantage to switch your choice? The host always opens a door with a goat behind it, but not the door you chose first, regardless of which door you chose first. You reserve the right to open the door you chose first, but can change to the remaining door after the host opens the door to reveal a goat. You get as a price the item behind the final door you choose. You prefer cars over goats (cars are worth 1 and goats are worth 0). The car is behind doors 1, 2, and 3 with probabilities P1, P2 and 1- P1 P2 respectively, and you know the values of p1 and 22. Please answer the following questions. 1. Model this problem using a decision network using the following variables. CarDoor {1,2,3} is the door such that the car is behind it. This is a random variable. Host Choice {smaller, bigger} is the index of the door picked by the host is the smaller or bigger one of the two left for them to pick. This is a random variable. FirstChoice {1,2,3} is your first choice of a door. This is a decision variable. SecondChoice {stay, switch} indicates whether you stay with the door you picked first or switch to the other door. This is a decision variable. Utility E {0,1} is 0 if you get a goat and 1 if you get a car. Car Door First Choice Host Choice Second Choice Utility Figure 1: The Monty Hall Problem The Monty Hall Problem is stated as follows. You are on a game show, and you are given the choice of three doors: Behind one door is a car; behind the others, goats. The host knows what's behind each door but you don't. First, you pick a door, say Door 1. Second, the host opens another door, say Door 3, which has a goat behind it. Finally, the host says to you, Do you want to pick Door 2?" Is it to your advantage to switch your choice? The host always opens a door with a goat behind it, but not the door you chose first, regardless of which door you chose first. You reserve the right to open the door you chose first, but can change to the remaining door after the host opens the door to reveal a goat. You get as a price the item behind the final door you choose. You prefer cars over goats (cars are worth 1 and goats are worth 0). The car is behind doors 1, 2, and 3 with probabilities P1, P2 and 1- P1 P2 respectively, and you know the values of p1 and 22. Please answer the following questions. 1. Model this problem using a decision network using the following variables. CarDoor {1,2,3} is the door such that the car is behind it. This is a random variable. Host Choice {smaller, bigger} is the index of the door picked by the host is the smaller or bigger one of the two left for them to pick. This is a random variable. FirstChoice {1,2,3} is your first choice of a door. This is a decision variable. SecondChoice {stay, switch} indicates whether you stay with the door you picked first or switch to the other door. This is a decision variable. Utility E {0,1} is 0 if you get a goat and 1 if you get a car. Car Door First Choice Host Choice Second Choice Utility Figure 1: The Monty Hall