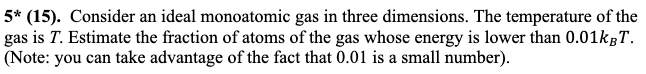
2. Fluctuations in the energy of a system that consists of many particles. By solving this problem you will discover a very important and deep mathematical fact that underlies many results in statistical mechanics: According to the Boltzmann distribution, the probability of, say, the kinetic energy of a particle belonging to a 2D ideal gas (or the probability that a money game participant has wealth equal to e) is proportional to exp(). Here T = (e) is the mean energy/money. This means that the actual value of e can vary quite a bit - it's not improbable that the molecule has, say, an energy of 3(e) or 0.3 (e). However, if we have a gas consisting of, say N = 1000 such molecules, their total energy will be very close to (E) = N(e) = 1000T, and finding the gas to have energy 3(E) or 0.3 (E) will be outlandishly improbable. This is why macroscopic objects consisting of large numbers of molecules behave predictably, while properties of individual molecules (such as their energies) fluctuate wildly. Here you get to investigate this phenomenon experimentally". First, generate, on a computer, an "ensemble" of N 1 molecules with their energies distributed according to the Boltzmann law. That is, the probability that a molecule's energy lies within e and + de is p(e)de = (+-) e/T de [To do so, you can use the following trick: Use your computer's random number generator to generate a set of random numbers x1, x2 ..., XN each drawn from a uniform distribution between 0 and 1. Then the set of energies defined by e = -T In x{ will obey the desired Boltzmann distribution (*Extra credit, 10 points: prove that!). You can think of e/T, generated this way, as the energy of a molecule measured in the thermal units (i.e. normalized by T).] A. Plot a histogram of energies of the molecules and verify that they obey the anticipated Boltzmann distribution. i=1 B. Now group your "molecules" in sets of ng = 3, 7, 20 and calculate the energy Eg = for each group. Plot the histogram of Eg (it is convenient to, again, use units where Eg is normalized by its mean value, that is consider the dimensionless energy variable Eg = Eg/(Eg). How does the distribution evolve as a function of the number ng of croup members, and what does it tell us about energy fluctuations in objects (groups) consisting of many molecules? (* Extra credit, 5 points: We claimed that Boltzmann applies to objects containing many molecules - why are your distributions not exponential then?) Note: You will likely need numerical software to accomplish these tasks. Examples include Mathematica, Matlab etc. Mathematica is free of charge to UT students, and we can help you with using it. 3. Yet another (non-cyclic) heat engine. Consider a cylinder containing an ideal gas under a piston, as shown in Figure below. After a weight m is removed from the piston, the gas expands, lifts the remaining weight m2, and the piston eventually settles at a new position h. A. Assuming that the above process is carried out in a room whose temperature is maintained constant so that the initial and the final temperature of the gas is exactly the same, what is the work W performed on the weight m2 in this process? B. What is the heat received by the gas in this process? C. Think about this contraption as a heat engine that receives heat from the surroundings and performs work. Does its operation contradict the 2nd law? (recall the formulation of the 2nd law that is concerned with heat engines). Explain your answer. D. What is the change of the Helmholtz free energy of the gas AA as a result of the process? E. Compare W with AA. Which one is greater? Is your finding consistent with the equation that we have derived in the class for the maximum work that can be performed by a system at constant temperature? vacuum m m ideal gas 5* (15). Consider an ideal monoatomic gas in three dimensions. The temperature of the gas is T. Estimate the fraction of atoms of the gas whose energy is lower than 0.01kBT. (Note: you can take advantage of the fact that 0.01 is a small number).