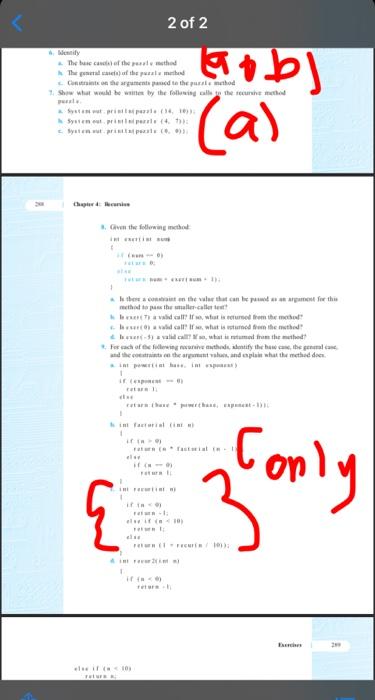
2 of 2 the back the method the of the peale med Cement the method 1 Show what would be inte ty the folleto te hem hobl (a) Nyten we Geen the following into + the the wall valid call it is reed from the call what is used for the the vaca, me the method For each of five the tify the habe gemale the contacters and plain what the method de In facta Conly in { ter TEINE mmg method: int puzzle(int base, int limit) { if (base > limit) return -1; else if (base-limit) return 1; else return base puzzle( base + 1, limit); } 6. Identify 1. The base case(s) of the puzzle method b. The general case(s) of the puzzle method e Constraints on the arguments passed to the puzzle method 7. Show what would be written by the following calls to the recursive method puzzle. 11. System out.println(puzzle (14, 10)): b System out.println(puzzle (4. 7)): e. System out.println(puzzle (0, 0)) 8. Given the following method: int exer(int num) { if (num - 0) return 0; else return num + exer(num + 1); 2. Is there a constraint on the value that can be passed as an argument for this method to pass the smaller-caller test? b. Is exer(7) a valid call? If so, what is returned from the method? c. Is exer(0) a valid call? If so, what is returned from the method? d. Is exor (-5) a valid call? If so, what is returned from the method? 9. For each of the following recursive methods, identify the base case, the general case, and the constraints on the argument values, and explain what the method does. 2. int power (int base, int exponent) if (exponent - 0) return 1; else return (base power (base, exponent - 1)); b. int factorial (int n) if (n > 0) return (n. factorial (n. 1)): else if (0) return 1: c. int recur(int n) if (n limit) return -1; else if (base-limit) return 1; else return base puzzle( base + 1, limit); } 6. Identify 1. The base case(s) of the puzzle method b. The general case(s) of the puzzle method e Constraints on the arguments passed to the puzzle method 7. Show what would be written by the following calls to the recursive method puzzle. 11. System out.println(puzzle (14, 10)): b System out.println(puzzle (4. 7)): e. System out.println(puzzle (0, 0)) 8. Given the following method: int exer(int num) { if (num - 0) return 0; else return num + exer(num + 1); 2. Is there a constraint on the value that can be passed as an argument for this method to pass the smaller-caller test? b. Is exer(7) a valid call? If so, what is returned from the method? c. Is exer(0) a valid call? If so, what is returned from the method? d. Is exor (-5) a valid call? If so, what is returned from the method? 9. For each of the following recursive methods, identify the base case, the general case, and the constraints on the argument values, and explain what the method does. 2. int power (int base, int exponent) if (exponent - 0) return 1; else return (base power (base, exponent - 1)); b. int factorial (int n) if (n > 0) return (n. factorial (n. 1)): else if (0) return 1: c. int recur(int n) if (n