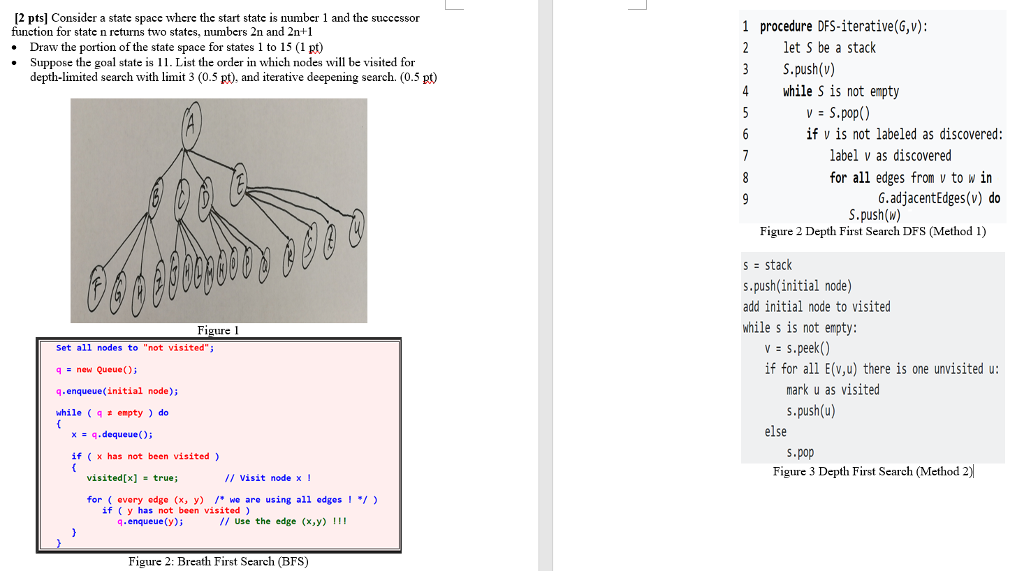
[2 pts] Consider a state space where the start state is number 1 and the successor function for state n returns two states, numbers 2n and 2n+1 . Draw the portion of the state space for states 1 to 15 (1 pt) . Suppose the goal state is 11. List the order in which nodes will be visited for 1 procedure DFS-iterative(G,v): 2 let S be a stack 3 S.push(v) 4 while S is not empty depth-limited search with limit 3 (0.5 pt), and iterative deepening search. (0.5 pt) v S.pop() if v is not labeled as discovered: label v as discovered for all edges from v to w in G.adjacentEdges(v) do S.push(w) Figure 2 Depth First Search DFS (Method 1) s stack s.push(initial node) add initial node to visited while s is not empty: Figure I v = s.peek() if for all E(v,u) there is one unvisited u: Set all nodes to "not visited" qnew Queue) q.enqueue(initial node); while qempty) do mark u as visited s.push(u) q.dequeue(); else x if ( x has not been visited) s.pop Figure 3 Depth First Search (Method 2) visited[x]- true; /I visit node x for ( every edge (x, y) /* we are using all edge ) if (y has not been visited) q.enqueue(y) / Use the edge (x,y)! Figure 2: Breath First Search (BFS) [2 pts] Consider a state space where the start state is number 1 and the successor function for state n returns two states, numbers 2n and 2n+1 . Draw the portion of the state space for states 1 to 15 (1 pt) . Suppose the goal state is 11. List the order in which nodes will be visited for 1 procedure DFS-iterative(G,v): 2 let S be a stack 3 S.push(v) 4 while S is not empty depth-limited search with limit 3 (0.5 pt), and iterative deepening search. (0.5 pt) v S.pop() if v is not labeled as discovered: label v as discovered for all edges from v to w in G.adjacentEdges(v) do S.push(w) Figure 2 Depth First Search DFS (Method 1) s stack s.push(initial node) add initial node to visited while s is not empty: Figure I v = s.peek() if for all E(v,u) there is one unvisited u: Set all nodes to "not visited" qnew Queue) q.enqueue(initial node); while qempty) do mark u as visited s.push(u) q.dequeue(); else x if ( x has not been visited) s.pop Figure 3 Depth First Search (Method 2) visited[x]- true; /I visit node x for ( every edge (x, y) /* we are using all edge ) if (y has not been visited) q.enqueue(y) / Use the edge (x,y)! Figure 2: Breath First Search (BFS)