Question: [20 marks] Consider the real, even vector f = [fo, f1, ..., fN-1], in which f = R, and fn = N-n (analogous to

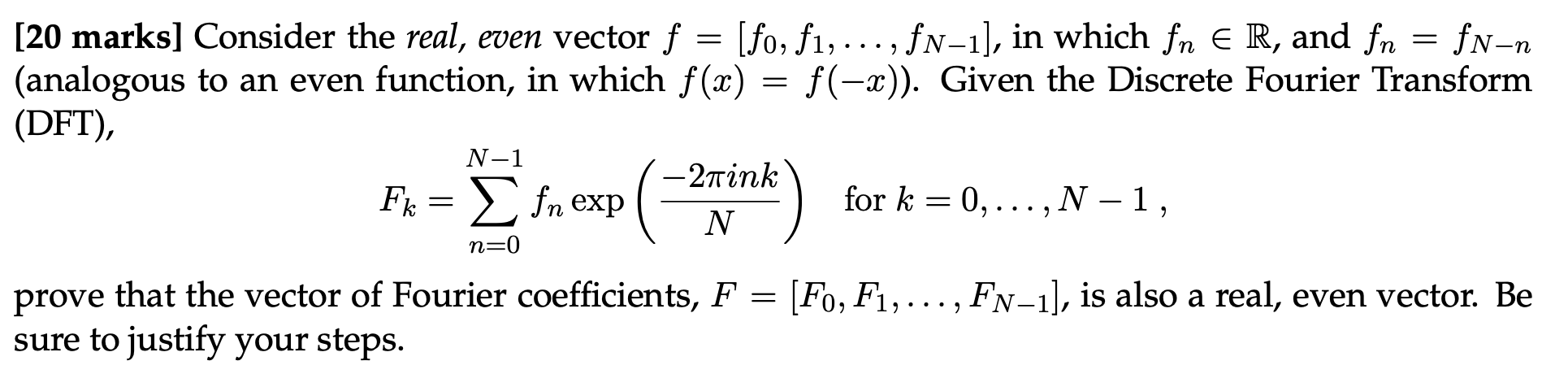
[20 marks] Consider the real, even vector f = [fo, f1, ..., fN-1], in which f = R, and fn = N-n (analogous to an even function, in which f(x) = f(-x)). Given the Discrete Fourier Transform (DFT), N-1 Fk = fn exp XP (-2wink) for k N = 0,..., N-1, n=0 prove that the vector of Fourier coefficients, F = [Fo, F1,..., FN-1], is also a real, even vector. Be sure to justify your steps.

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

For the frame and loading shown, determine the internal forces at the point indicated: Point K. 80 mm80 mm 20 mm 20 mm 20 mm 40 mm 250 N C 250 N

Briefly describe ASCII and Unicode and draw attention to any relationship between them. [3 marks] (b) Briefly explain what a Reader is in the context of reading characters from data. [3 marks] A...

Let A, B be sets. Define: (a) the Cartesian product (A B) (b) the set of relations R between A and B (c) the identity relation A on the set A [3 marks] Suppose S, T are relations between A and B, and...

QUIZ... Let D be a poset and let f : D D be a monotone function. (i) Give the definition of the least pre-fixed point, fix (f), of f. Show that fix (f) is a fixed point of f. [5 marks] (ii) Show that...

QUESTION #3 X Company acquired 70% of the Y Company on December 31%2022 at a cost of C$1,400,000. Y is based in Italy. The book values of Y's assets and liabilities were equal to fair values o the...

1456HHSC attend all (a) In the quantum teleportation protocol, Alice and Bob are every in possession of one qubit of a couple in the joint country00i + statei. Explain how the protocol works. In...

Problem 1): Branches: Delay Slot and Hazards Consider a 6-stage MIPS pipelined processor with the following stages: IF, ID, EX, BR, MEM, WB. In the BR (Branch Resolution) stage, both the branch...

(a) In SystemVerilog, what is the difference between: (i) The ternary operator ? and if...then...else statements? [2 marks] (ii) always_ff and always_comb? [2 marks] (iii) Blocking, non-blocking and...

answer the question clearly You are building a flight-control system for which a convincing safety case must be made. Would you assign the tasks of safety requirements engineering, test case...

You are designing a new syntax for a programming language like Java, with the intention of making it more approachable to students by using English words instead of punctuation symbols. (a) How does...

In a Hopfield neural network configured as an associative memory, with all of its weights trained and fixed, what three possible behaviours may occur over time in configuration space as the net...

The National Basketball Association calculates many statistics, just like any other professional sport. Average points per game, average rebounds per game, number of years played, number of titles,...

Compute the first and second derivatives for the following table of data at x = 1.1 1.0 X Y 1.2 0.000 0.128 1.4 0.544 1.8 1.6 1.296 2.432 2.0 4.000

1 Multiple Choice 1 point All of the following are disadvantages of an ERP system except ERPs - frequently cause organizations to change their business processes to standardized ones. an ERP provides...

10 landmark judgement of limitations act, 1963. Judgements + case briefs. Particularly for india.

Question: A company is considering drilling an outpost well. Wellsite preparation, drilling and testing of the well is expected to cost $2 million. Completion of the well and the field equipment...

1. Find the mutual inductance of the following system if the straigth conductor is infinitely long (35)

Lucid Images Ltd manufactures premium high definition televisions. The firms fixed costs are$4,000,000 per year. The variable cost of each TV is $2,000, and the TVs are sold for $3,000 each. The...

5.(a). In a Normal" atmosphere, what is the ratio of the distance to the radio horizon to the distance to the geometrical horizon? Explain briefly why the ratio is not 1. [4]

Design a minimum-mass symmetric three-bar truss (the area of member 1 and that of member 3 are the same) to support a load P, as was shown in Fig. 2.9. The following notation may be used: Pu = P cos...

=+changes was 11.45 lb. Is there sufficient evidence to conclude that the true mean change in weight is positive? Use a 5 .05.

=+to conclude that the proportion very satisfied is different for elementary school teachers than it is for high school teachers? Test the appropriate hypotheses using a .05 significance level.

=+Three hundred twenty-two subjects, selected at random from those who successfully participated in a program to quit smoking, were weighed at the beginning of the program and again 1 year later. The...